1首先在带权无向图的邻接矩阵中,行数和列数分别代表顶点数和边数,因此需要先确定图的顶点数和边数2其次根据顶点数和边数,初始化一个二维数组作为邻接矩阵,将矩阵中的所有元素初始化为0或无穷大,表示没有边连接3最后填充邻接矩阵,根据图的边权值,将邻接矩阵中的对应元素填充为实际的;弱连通表示将所有边视为无向时,所有节点间存在路径邻接矩阵描述任意节点间的连接关系无向图的邻接矩阵为对称二值矩阵有向图的邻接矩阵为不对称二值矩阵带权图的邻接矩阵为带权的邻接矩阵数据集可以转换为图结构表现形式,基于样本数据相似度构建;Floyd算法的核心在于通过一个图的权值矩阵求出它的每两点间的最短路径矩阵从图的带权邻接矩阵A开始,通过递归地进行n次更新,即由矩阵D0=A,按公式构造出矩阵D1,再由D1构造出D2,直至构造出Dn,最终得到的矩阵Dn即为图的距离矩阵,同时记录两点间的最短路径此过程利用了;对于节点A,其列表可能包含与B相连,边权重为5与C相连,边权重为3对于节点B,其列表可能包含与A相连,边权重为5与D相连,边权重为2以此类推,我们可以为每个节点创建一个类似这样的列表使用邻接表表示无向带权图的优点在于它能够高效地表示图的结构相比于使用邻接矩阵,邻接表只存储实际。
带权无向图的邻接矩阵是一种表示图中顶点之间关系的数据结构它的特点如下1对称性带权无向图的邻接矩阵是一个对称矩阵,即矩阵的第i行第j列的元素与第j行第i列的元素相等这是因为在无向图中,如果顶点i与顶点j之间存在一条边,那么顶点j与顶点i之间也一定存在一条边2对角线元素为0;如图所示点击下图,可查看大图;1先把要讲解的图在下面展示一下,先看一下2然后在图中的邻接点的值的范围画出邻接表的表头3根据上一步画出的表头分析与其相连的点,这里链表之中后面有3个框4在链表中第一个框写相连点的顶点值,第二个框中写权值5根据上述的方式,依次把后面数字的链表写下来,无向带权图的。
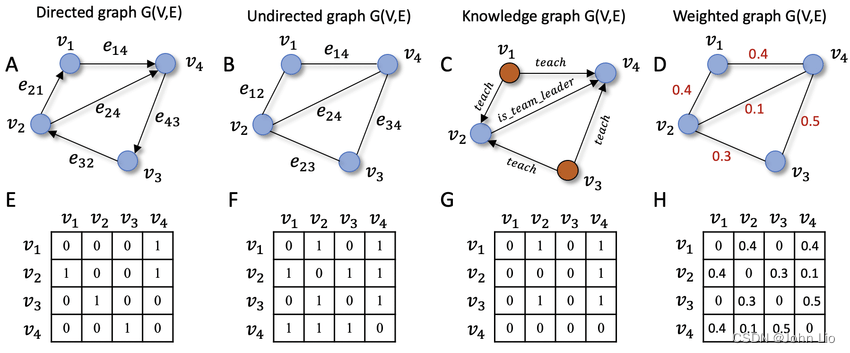
在一个顶点集合中,若两个顶点m和n之间存在直接的边,则在邻接矩阵中对应的位置上,我们可以赋予一个权值V,这个权值可以有不同的意义通常情况下,V可以是1,仅仅表示两点之间存在直接的连接关系当然,V也可以是两点之间的距离或费用等,具体取决于实际应用场景在邻接矩阵中,矩阵的每个元素am;假设有一个有向图G,包含n个顶点,我们可以用一个n×n的二维矩阵A来表示这个图的邻接关系和边的权重矩阵A的行和列分别对应图G的顶点,矩阵元素Aij的值表示从顶点i到顶点j的边的权值如果图中不存在从顶点i到顶点j的边,则Aij可以设为无穷大或特定的标记值,表示没有连接例如;不带权的时候,1表示两个点连通,0表示不连通带权的时候,连通的两点,矩阵中的值为两点间的权值点和点自身标为0不连通的两点的值为无穷;图论是研究顶点和边连接关系的数学分支邻接矩阵和邻接表是图的两种常见表示方法拓扑排序是针对有向无环图的一种顶点排序方式图论 定义图论的核心在于描述顶点和边的连接关系无向图由非空顶点集和无序边集组成,有向图则在边集中使用笛卡尔积来表示方向性带权图则为每条边赋予权重 基本。
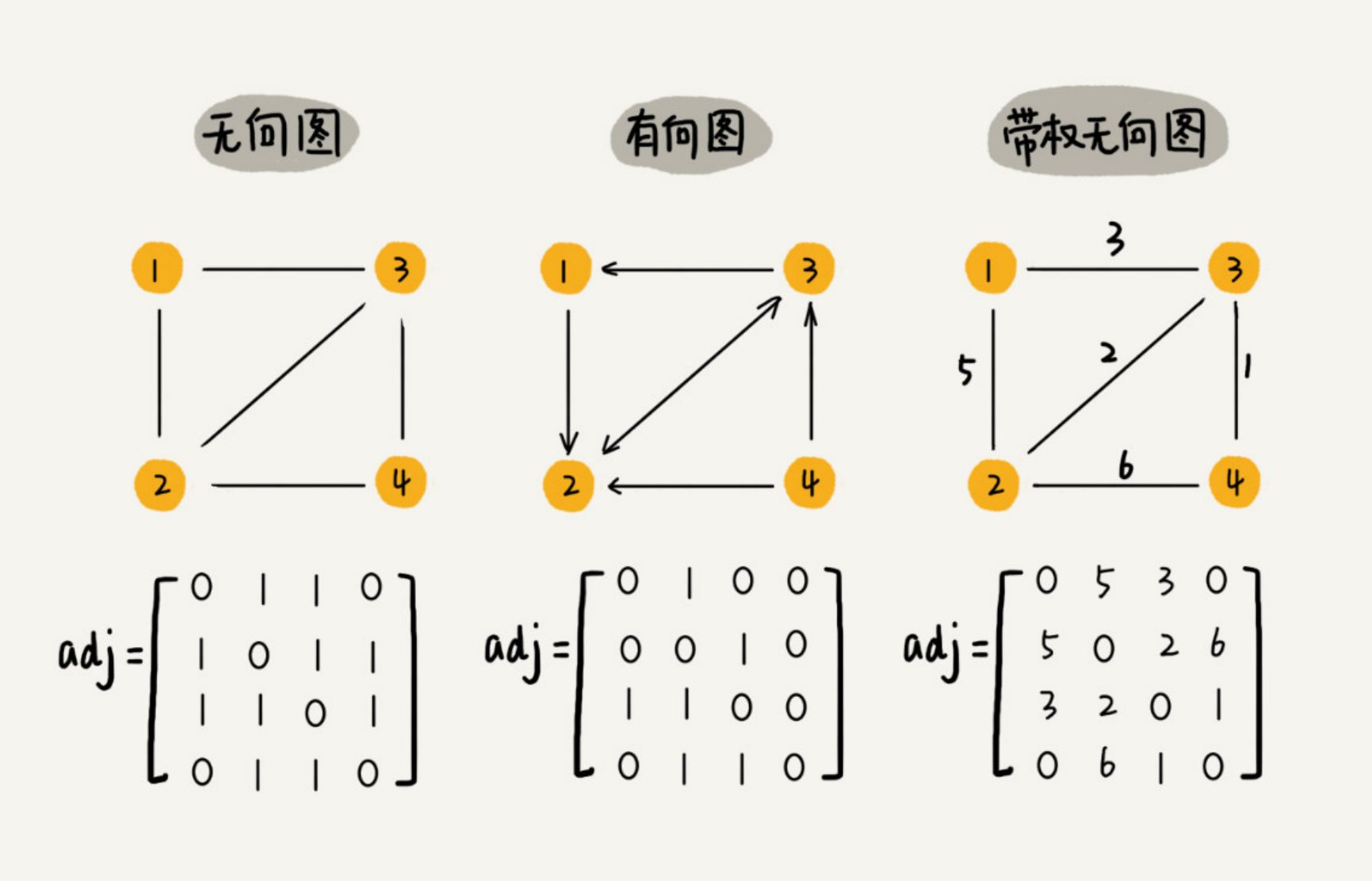
无向图的邻接矩阵一定是对称的,而有向图的邻接矩阵不一定对称因此,用邻接矩阵来表示一个具有n个顶点的有向图时需要n^2个单元来存储邻接矩阵对有n个顶点的无向图则只存入上下三角阵中剔除了左上右下对角线上的0元素后剩余的元素,故只需1+2++n1=nn12个单元无向;N = 4 图中的节点数目dag = zerosN,N邻接矩阵初始化,值均为0C = 1 S = 2 R = 3 W = 4制定各节点编号dagC,R S = 1有两条有向边CR,CSdagR,W = 1有向边RWdagS,W=1有向边SW;入度入边的数量则由第i列的元素之和给出值得注意的是,由于无向图的邻接矩阵对称且对角线为零,实际存储时可以只保留上三角或者下三角部分,因为另一半是重复的因此,对于无向图,存储邻接矩阵所需的总空间是nn12,而非n^2这个优化在处理大型图时尤为重要,能够节省存储空间。
对于任意两个节点m和n,如果它们之间存在直接连接,那么在邻接矩阵中,对应位置的元素amn也等于anm会包含一个特定值,这个值被称为权重权重的具体含义可以根据实际情况来定义例如,如果两个节点之间仅仅是可达,那么权重可以设为1如果权重代表两点之间的距离,则可能是一个具体的;有带权图的邻接矩阵里面有0带权图的邻接矩阵可以用0表示,也可以用最大值表示矩阵中的每一个1代表两个顶点邻接存在一条边0代表不邻接,一条边代表两个1自己指向自己的顶点可以表示为0。