通过将目标函数对XA求偏导并另偏导等于0,我们就可以求出最优风险组合的权重解如下85XB=1XA86将数据代进去,就可得到最优风险组合的权重为=04XB=104=06该最优组合的预期收益率和标准差分别为该最优风险组合的单位风险报酬=11%5%142%=042有效边界的表达式。
求解第一步,求风险资产的最优组合及该组合的收益率与标准差随意指定一个期望收益率,考虑达到的最小方差的投资比例因为无风险证券的方差以及与其他风险证券的协方差也都等于零,所以包括无风险证券在内的投资组合的方差实际上就等于风险证券组合的方差min,令L=+,由一阶条件。
最优风险组合是指投资者通过合理配置不同类型的资产,以实现风险最小化与收益最大化平衡的组合解释如下1 风险与收益的平衡 最优风险组合的核心在于平衡风险与收益投资者在追求投资回报的同时,也关注资金的安全性和波动性最优风险组合旨在找到一种资产配置方案,使得投资者在可承受的风险范围内。
M点作为所有证券以各自的总市场价值为权数的加权平均组合,它是有效市场组合的代表在马科维茨的资产组合理论中,M点提供了最高的风险收益比,适合所有正常投资者理论上,所有投资者在考虑风险和收益期望一致的情况下,都会选择M点作为最优组合尽管理论中假设了一个理想化的世界,但在现实世界中,我。
其次,你的资产组合仅仅包括两种风险资产和一种无风险资产,而且你要知道两种风险资产的期望收益率风险和相关系数,还要知道无风险资产的预期收益率 那么,根据Harry M Markowitz的资产组合理论,我们可以得到类似于下面的这幅图,图中曲线为两种风险资产的组合情况,曲线上不同的点代表了投资两种资产的不同比重图中直。
在金融领域,证券市场线斜率是一个重要的概念,它表示了风险与收益之间的关系两点确定一条直线,已知的两个点是无风险利率0%,6%和最优风险资产组合22%,14%通过这两个点,可以计算证券市场线的斜率计算方法如下首先,确定两点间的收益差,即14% 6% = 8%其次,确定两点间的。
最优风险投资组合是投资者在选中的各种可能的投资组合中,可以获取效益最大化的一种投资组合形式,一般是指在证券股票基金等,市场在各种证券集合的过程中,根据每一个证券的风险回报率未来发展趋势等,选择相互能产生正作用的投资产品及形式一般选择有效集的上凸性和无差异曲线的下凹性决定了最。
最优投资组合是通过综合考虑风险与收益,结合投资者的投资目标风险承受能力投资期限等因素,选择的最合适的资产组合一理解投资组合的核心要素 确定最优投资组合的首要任务是理解其核心要素投资组合的主要目标是实现投资的多元化,以分散风险并寻求最佳的收益这涉及到对各类资产的理解,以及它们之间。
是一些非常合理的计算数据用户可以根据数据之间的关系,来判断资本市场各个数据的走向,以此,算到自己想要得到的结论一资本市场线在期望收益率为纵轴,资产标准差为横轴的平面上,风险资产的有效集是一个弧纵轴上的无风险利率点作为风险资产有效弧上方的切线,该切线点称为最优风险组合,或市场组合。
最优投资组合的确定涉及多个因素的综合考量,包括投资者的风险承受能力投资目标投资期限以及市场状况等解释如下1 投资者风险承受能力每个投资者的风险承受能力是不同的,这是决定投资组合的重要因素之一高风险承受能力的投资者可以选择更多投资于股票等高风险资产,以获得更高的潜在回报而风险。
解析式推导 首先,我们定义n个资产的收益率和风险,其中风险用方差衡量,收益率用期望值表示,资产间的联动关系通过协方差表征投资组合通过n个资产的权重构建,组合的收益率和方差可以求得将随机生成的权重分配绘制成图,发现存在一个边界,即为“有效边界”目标是求解有效边界的解析式我们发现,在。
它的意义是单位风险获得的收益,值越大,越好在无风险资产与有效前沿的所有组合中,与切点T的Sharpe Ratio最大这就意味着,无风险资产与切点T的组合,在同等风险水平下,能获得的收益是最大的我们把T称为最优风险资产组合这条线被称作资本配置线CAL7 CAL成为新的有效前沿如果允许以。
与该投资者的最优风险资产组合无关投资者需要做的只是根据风险偏好确定最佳资产组合中无风险资产与风险资产组合的各自比例根据假定,投资者对风险资产的预期收益率方差和协方差有相同看法,即线性有效集对所有投资者来说都是相同的每一个投资者的投资组合都包括一个无风险资产和相同投资组合M,剩。
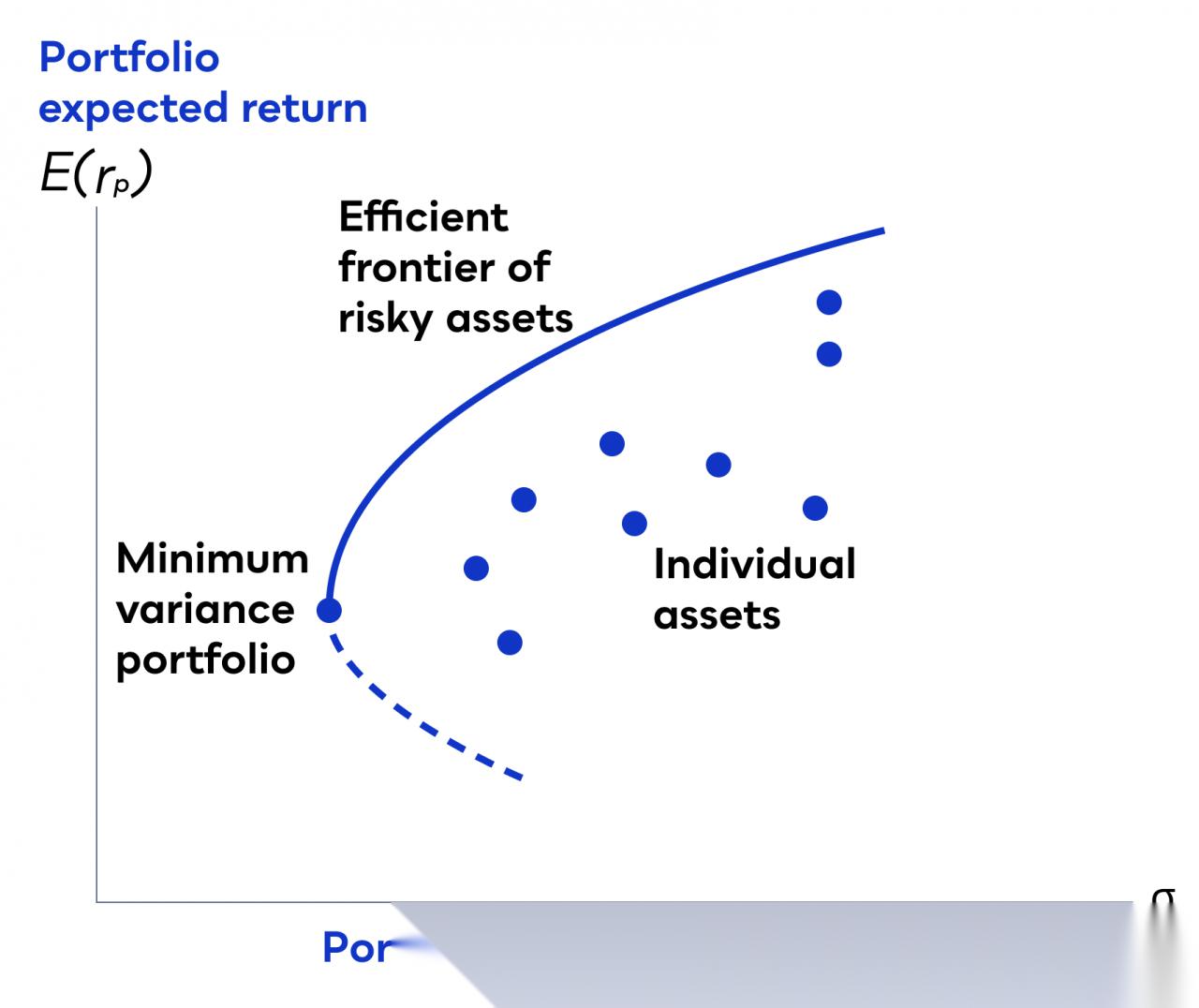
投资组合的有效前沿曲线马科维茨模型的核心是通过有效前沿曲线来描述不同风险水平下的最优资产组合有效前沿曲线是一条连接所有最优资产组合的曲线,使得在给定风险水平下,该组合的预期收益率最高有效前沿曲线可以通过不同的风险水平来绘制,其中最低风险组合点是在风险水平最低的情况下所能达到的最高。
风险预算的目标是实现最大单位风险收益,这一概念在CFA考试中尤为重要计算公式中,MCTR的定义是当某资产权重发生微小变化时,组合整体风险的边际变化,而ACTR则表示该资产在组合中总风险贡献的绝对值通过求导和数学推导,我们可以理解MCTR与ACTR的计算方法,并在实际应用中进行资产配置优化具体推导过程。
当可以自由借贷时,投资者可以通过调整无风险资产和风险资产的比例来优化自己的投资组合这一过程是线性的,因此最优的投资组合点也自然形成一个明确的边界分离定理不仅简化了投资决策过程,还为投资者提供了清晰的投资指导它表明,即使投资者对风险有不同的看法,他们仍然可以找到一个共同的最优投资。
