加权最小二乘法平差方法是一种针对不同点具有不同权重的数据集的平差方法其思路是将不同点的误差加权,从而更准确地评估出测量数据的误差权重通常是根据已知点的精度确定的3 最小平方平差法 最小平方平差法是一种该方法的目标是在满足约束条件的基础上,使每个方程的平方和之和最小化在。
步骤2根据初始估计结果,利用特定的公式式计算权重矩阵这个权重矩阵反映了不同测量数据在最终估计中的相对重要性,是WLS算法的核心部分最终估计与精度量化使用计算得到的权重矩阵,对目标位置进行最终的加权最小二乘估计通过估计结果的协方差矩阵来量化定位精度,从而评估算法的性能算法表现在。
推导加权最小二乘法在最小二乘法的基础上,考虑了不同数据点的权重权重通常根据数据点的精度来确定,精度越高的数据点赋予更大的权重通过加权处理,可以更准确地评估测量数据的误差,并求解出更精确的未知点坐标最小平方平差法推导最小平方平差法的目标是在满足特定约束条件的前提下,使。
呃,楼上是个广告男加权最小二乘WLS最一般的用法是克服异方差比方说,现在有一个多元回归y = bX + e矩阵表示,X#39代表矩阵X转置原来的一般最小二乘OLS公式是 b = X#39X^1 * X#39y 而在异方差情况下,由于不满足OLS的五大假定,因此OLS的结果不再有效not。
不是因为加权最小二乘法WLS会根据变异程度的大小赋予不同的权重,使其加权后回归直线的残差平方和最小,从而保证了模型有更好的预测价值加权最小二乘法是对原模型进行加权,使之成为一个新的不存在异方差性的模型,然后采用普通最小二乘法估计其参数的一种数学优化技术。
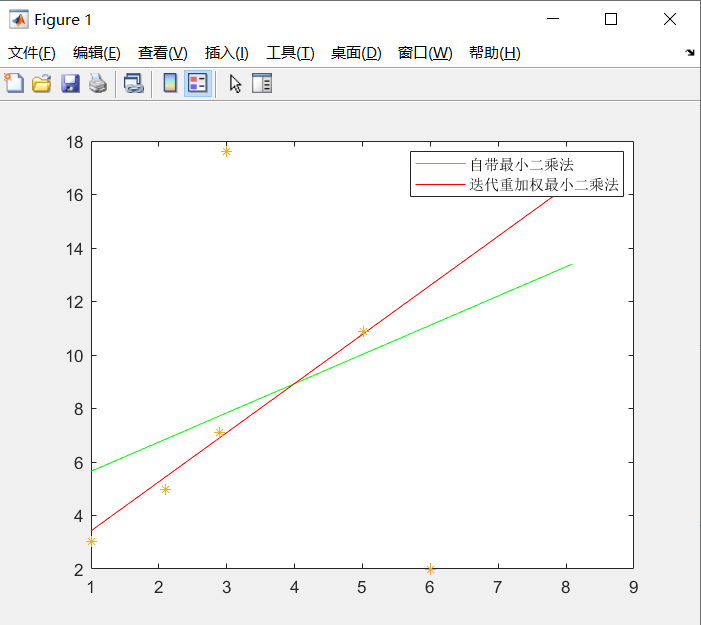
加权最小二乘法的实现过程与普通最小二乘法类似,但需要考虑权重因素具体来说,设有一组数据点x_i, y_i,其中i=1,2n,以及一组对应的权重w_i我们的目标是找到一个函数fx,使得加权误差的平方和最小,即Sigmaw_i * y_i fx_i^2达到最小通过求解这个。