TOPSIS是逼近理想解排序法,其原理是计算每个方案与理想解和负理想解的距离理想解是所有方案中最好的解,负理想解是最差的解计算TOPSIS值时,首先确定理想解和负理想解,然后计算每个方案到理想解和负理想解的距离,最后计算每个方案的相对接近度这个相对接近度就是最终的评价结果计算公式为相对接。
TOPSIS算法是一种多目标决策分析中的排序方法,主要通过评估对象与理想化目标的距离来确定优劣以下是TOPSIS算法的简单概括评价矩阵构建对m个评价目标和n个指标进行打分,形成评价矩阵规范化处理对评价矩阵进行规范化处理,生成规范化向量和规范化矩阵,以及权重规范化矩阵确定理想解与反理想解根。
TOPSIS法是一种综合评价方法,能充分利用原始数据信息,计算评价对象与最优最劣方案的距离,以此评估优劣方法步骤包括正向化标准化计算距离得分排序12 适用范围 适用于已知评价对象得分及指标值13 基本步骤 将原始数据正向化标准化,计算距离,排序得分2 案例分析 通过评估各风景地。
TOPSIS综合评价法是一种在多目标决策分析领域中广泛应用的有效工具,通过计算评价对象与理想化目标的接近程度来进行相对优劣排序的评价分析手段以下是TOPSIS综合评价法的核心要点基本原理TOPSIS法,全称为优劣解距离法,其核心在于确定评价对象与理想解和负理想解的相对距离,从而判断各评价对象的优劣评。
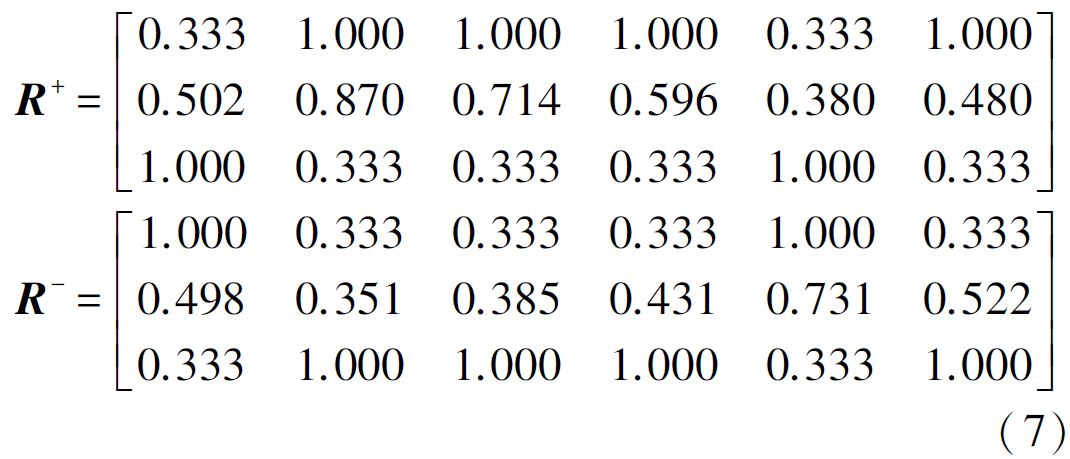
TOPSIS法首先找出评价指标的正负理想解值A+和A,接着计算出各评价对象分别与正负理想解的距离值D+和D根据D+和D值,最终计算得出各评价对象与最优方案的接近程度C值,并可针对C值进行排序最终从上表可知评价对象4,即开发区4,它的相对接近度C值最高为09995,因而说明开发区4在。

TOPSIS优劣解距离法是一种数据处理和数据分析中的评估方法其基本操作基于归一化后的原始数据矩阵,通过余弦法找出最优方案与最劣方案,计算评价对象与最优方案和最劣方案的间距,以此作为评价优劣的依据TOPSIS法适用于数据处理和数据分析领域TOPSIS法包含三个主要步骤首先,对原始数据进行同趋势化。
TOPSIS法涉及矩阵构建指标正向化标准化计算得分和结果处理等步骤模型步骤具体如下构造评价指标矩阵,描述所有指标指标正向化,统一指标类型,转换为极大值指标标准化处理,消除不同指标量纲影响计算得分,定义与最大值最小值的距离,结合权重计算得分结果处理,归一化或标准化,便于比较。
如身体健康评估体温正向化矩阵标准化,消除不同指标量纲影响,标准化方法多种,如公式标准化,主要去量纲计算得分并归一化,定义最大值最小值,计算距离,第n个对象与最大值最小值距离决定得分,得分归一化保持排序不变简化后,TOPSIS法通过正向化标准化计算得分实现综合评价。
TOPSIS模型的算法步骤包括数据预处理数据规范化构建加权矩阵确定正理想解和负理想解计算距离计算排队指标值以及按指标值排序以研究生院评估为例,首先对师生比区间型数据和其他属性数据进行规范化处理,得到规范化后的数据接着,根据设定的权重值对数据进行加权,找到正理想解和负理想解。
首先,熵权TOPSIS法强调了权重分配的合理性,它根据信息熵理论,为各个评价指标赋予适当的权重,使评价更为全面和精确在实证过程中,将学生各科成绩转化为相应的评价指标,然后通过计算每个学生在各维度上的相对优势和劣势,形成一个综合的排序接着,熵权TOPSIS法通过建立理想解和负理想解,将学生分数与。
通过正向化处理和标准化,TOPSIS算法将数据转化为统一格式,便于计算然而,实际操作中还需注意不同指标的权重分配,以及如何根据问题背景确定权重尽管TOPSIS有其局限,如对数据的依赖,但在建模过程中,灵活运用和合理调整是解决问题的关键作业部分,我将实际案例和PPT中的内容展示出来,帮助理解TOPSIS在。
TOPSIS法,全称为逼近理想解排序法,是一种综合评价方法,特别适用于多组评价对象,通过衡量对象与最优解和最劣解的距离进行排序其步骤包括原始矩阵正向化标准化计算得分和归一化在正向化过程中,指标分为四种类型极大型极小型中间型和区间型标准化消除不同量纲影响,确保评价过程公平计。
7计算接近度指数根据距离度量计算每个评估对象的接近度指数接近度指数可以确定为与负理想解距离比上与理想解距离与负理想解距离之和8排序按照接近度指数的大小对评估对象进行排序,从而得到最终的排名结果需要注意的是,Topsis方法在应用时需要明确决策者的偏好和权重设置,以确保评估结果符合实际。
举例来说,假设我们有一组学生,我们希望根据学生的成绩表现和其他因素对他们进行综合评价我们可以使用TOPSIS法来进行这个评价首先,我们需要确定理想化的最优解,也就是在所有学生中表现最好的学生然后,我们需要确定最劣解,也就是在所有学生中表现最差的学生接下来,我们会计算每个学生与这两。
TOPSIS法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法它通过归一化后的数据规范化矩阵,找出多个目标中最优目标和最劣目标分别用理想解和反理想解表示 ,分别计算各评价目标与理想解和反理想解的距离,获得各目标与理想解的贴近度,按理想解贴近度的大小排序,以此作为。
紧接着,我们构建加权规范矩阵,以反映各指标权重计算正理想解与负理想解,通过比较获取最优与最劣方案计算方案到正负理想解的距离,以量化方案与理想状态的偏离程度最终,通过计算排序指标值,实现方案排序实例中以数学建模算法与应用中司守奎的案例为例,详细演示了TOPSIS法的应用流程与计算。
4 **SPSSAU分析**完成数据处理后,使用熵权法计算权重,生成新数据newdata接着,应用newdata进行TOPSIS法分析,计算各评价对象与理想解的距离,最终得到各对象的接近程度C值,从而确定最优方案5 **结果解释**通过熵权法计算的权重和新数据newdata,分析得出各个对象的C值例如,根据计算结果。
该方法利用归一化后的原始数据矩阵,通过余弦法找出最优方案和最劣方案,进而计算各评价对象与最优方案和最劣方案的距离,以此评估各对象的优劣TOPSIS法操作简便,对数据分布和样本含量无严格限制例如,小明在数学考试中获得134分,如何判断这个成绩是好还是不好TOPSIS法可以给出答案首先,根据指标。