1 KMOKaiserMeyerOlkin值是评估变量间相关性矩阵是否适合进行因子分析的一个度量通常,KMO值大于07被认为适合进行主成分分析2 当进行主成分分析时,KMO值大于07意味着数据非常适合进行因子分析,这表明变量之间存在较强的相关性,适合提取公因子3 如果KMO值在06到07之间,虽然可。
答案主成分分析并没有严格规定KMO值必须大于07但通常情况下,KMO值大于07被认为适合进行主成分分析解释1 KMO值的意义KMO值是KaiserMeyerOlkin的样本充分性检验值,用于评估数据是否适合进行主成分分析其值范围在0到1之间,越接近1表示数据越适合进行主成分分析2 一般建议在实际。
并非所有的数据都适用于主成分分析的主成分分析本身并不是目的, 实际应用中主成分分析往往是一种手段目的是通过主成分分析简化数据结构, 在此基础上进行进一步的分析因此, 使用主成分分析的前提条件是原始数据各个变量之间应有较强的线性相关关系如果原始变量之间的线性相关程度很小, 它们之间不存在。
主成分分析中的KMO值通常被用来评估因子分析的效度文献中建议,KMO值在09以上被认为是进行因子分析的理想范围,08到09之间是适宜的,07到08则勉强接受,而06到07被认为是尚可的当KMO值低于06,研究质量就会有所下降,低于05则通常建议放弃该分析我自己的经验是,即使KMO值在0。
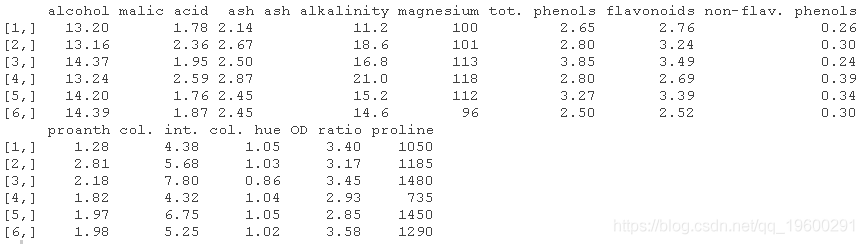
原始数据主成分分析是一种基于数据的降维技术,其目的是将高维数据转换为低维数据,从而减少数据的维度,并保留原始数据中的主要信息,用平均值会导致数据的变化被平滑化,从而损失数据的一些细节信息,所以主成分分析用原始数据。
如果主成分分析kmo检验低于05,而p值小于005能用主成分分析吗一般需要都满足分析要求,数据才适合分析KMO和巴特球形检验 分析KMO值如果此值高于08,则说明非常适合进行因子分析如果此值介于07~08之间,则说明比较适合进行因子分析如果此值介于06~07,则说明可以进行因子分析如果。
在吴明隆统计实务一书中,提到KMOKaiserMeyerOlkin检验的值通常需要大于05,以确保数据的多元性适合进行主成分分析PCA此外,方差贡献率至少达到40%,被认为是进行PCA分析的一个最低可接受标准。
四图像和视频处理 主成分分析在图像和视频处理中也有广泛的应用例如,PCA可以用于图像压缩和降噪,通过提取图像的主要成分来减少数据的维度,从而实现图像的压缩和降噪效果此外,PCA还可以用于人脸识别等任务总结来说,主成分分析作为一种重要的数据分析工具,广泛应用于高维数据处理特征提取和选择。
主成分分析法适用于变量间有较强相关性的数据,若原始数据相关性弱,则起不到很好的降维作用,降维后,存在少量信息丢失,不可能包含100%原始数据主成分分析是一种统计方法,即通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分主成分分析首先是由K。
KMO做主成分分析效度检验指标KMO09上非常合适做因子分析0809之间适合0708之间适合0607之间尚0506之间表示差05下应该放弃操作方法如下1首先打开要分析的SPSS文件或导入数据,选择相应数据,打开2接下来选择“分析”中“降维”里的“因子”3在弹出的。
主成分分析与主成分得分表达式的区别主要体现在分析目的数学表达与应用阶段在进行主成分分析前,首先需判断数据是否适合进行主成分分析,通常通过KMO值与Bartlett的检验来评估数据适配性当KMO值大于06且数据通过球形度检验时,可进行主成分分析主成分分析目的在于信息浓缩,并寻求主成分与分析项之间的。
主成分分析结果解读中,KMO值和Bartlett检验用于评估数据的适用性在本例中,由于KMO值和p值满足要求,数据适合进行主成分分析特征值和方差解释率帮助我们理解主成分的重要性,碎石图则直观显示了主成分的构成载荷系数和共同度衡量了主成分与指标之间的关系,共同度较高表明主成分解释能力强在本案例中。
一性质不同 1主成分分析法性质通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量2因子分析法性质研究从变量群中提取共性因子的统计技术二应用不同 1主成分分析法应用比如人口统计学数量地理学分子动力学模拟数学建模数理分析等学科中均。
时间序列分析通常关注数据随时间的变化,适用于如公司十年内月销售量数据的分析而主成分分析更适合用于面板数据,即在同一时间点收集的多项指标,如某一年的销售量资金流量主营业务收入等通过主成分分析,可以提取主要成分,并分析它们对原始数据的解释程度,随后可进行回归分析等进一步的统计处理3。
因子分析对于因子分析,可以使用旋转技术,使得因子更好的得到解释,因此在解释主成分方面因子分析更占优势其次因子分析不是对原有变量的取舍,而是根据原始变量的信息进行重新组合,找出影响变量的共同因子,化简数据主成分分析第一如果仅仅想把现有的变量变成少数几个新的变量新的变量几乎带有。
主成分分析方法适用的研究方面一数据分析与处理 主成分分析是一种常用的数据分析方法,广泛应用于数据预处理和特征提取阶段它能够将多个变量转化为少数几个主成分,从而简化数据结构,揭示变量之间的内在关系二多变量问题研究 在多变量问题的研究中,主成分分析发挥着重要作用在多指标评价体系中。