高斯定理Gauss law也称为高斯通量理论Gauss flux theorem,或称作散度定理高斯散度定理高斯-奥斯特罗格拉德斯基公式奥氏定理或高-奥公式通常情况的高斯定理都是指该定理,也有其它同名定理高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中因为。
Maxwell 方程描述为 ·B =0 41上式又称为磁场的高斯定律,表示任意磁场的散度为 0 ,即通过任意闭合曲面的净磁通总是 0 ,磁力线总是闭合的;电磁场的性质特征及其运动变化规律由麦克斯韦方程组确定地磁场 geomagnetic field 从地心至磁层顶的空间范围内的磁场地磁学的主要研究对象人类对于地磁场存在的早期认识,来源于天然磁石和磁针的指极性磁针的指极性是由于地球的北磁极磁性为S极吸引着磁针的N极,地球的南磁极磁性为N极吸引;3描述了变化的磁场激发电场的规律4描述了变化的电场激发磁场的规律麦克斯韦方程都是用微积分表述的,具体推导的话要用到微积分,高中没学很难理解,我给你把涉及到的方程写出来,并做个解释,你要是还不明白的话也不用着急,等上了大学学了微积分就都能看懂了1安培环路定理,就是;磁感线,亦称为磁力线,是法拉第首先发明并引入的物理概念它们在磁场中以曲线形式描绘,任何一点的曲线切线方向与该点的磁场方向相同,且磁感线互不交叉磁感线的闭合曲线特性在电磁学中尤为重要,这一特性通过Maxwell方程中的高斯定律得以描述磁力线的定义形象地描绘了磁场的分布,其中磁感应强度的方向;麦克斯韦第三方程,即法拉第电磁感应定律,揭示了变化的磁场能够产生电场,即电磁感应现象这一方程表明,当磁场强度随时间变化时,会在周围空间中产生电场,从而导致电荷的运动麦克斯韦第四方程,即高斯磁通定律,说明了磁通量在任何闭合曲面上的通量总是零,即磁力线不会闭合在任何封闭路径内这一方程;闭合回路这一现象在电磁学中称为磁通连续性定理,由 Maxwell 方程描述为 B =0 41上式又称为磁场的高斯定律,表示任意磁场的散度为 0 ,即通过任意闭合曲面的净磁通总是 0 ,磁力线总是闭合的同电流类似,磁力线总是走磁阻最小磁导率最大的路径,因此磁力线通常呈直线或曲线,不存在呈;高斯定理Gauss#39law表明在闭合曲面内的电荷分布与产生的电场之间的关系高斯定理在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定物理量,例如引力或者辐照度静电场与磁场,两者有着本质上的区别在静电。

磁场强度的计算公式H = N × I Le 式中H为磁场强度,单位为AmN为励磁线圈的匝数I为励磁电流测量值,单位位ALe为测试样品的有效磁路长度,单位为m概念磁场强度是线圈安匝数的一个表征量,反映磁场的源强弱磁感应强度则表示磁场源在特定环境下的效果 打个不恰当的比方;麦克斯韦方程组,被誉为最美的公式,是电磁学的基石,统一了电和磁,为后续科学理论的发展奠定了基础本文从广义的Stokes#39 定理的角度,解析麦克斯韦方程组,以深入理解这一物理学宝典理解麦克斯韦方程组的关键在于其整体结构和对称美方程组包含4个方程,分别涉及积分和微分形式积分形式适用于对称几何;在电动力学里,洛伦兹力Lorentz force是运动于电磁场的带电粒子所受的力根据洛伦兹力定律,洛伦兹力可以用方程,称为洛伦兹力方程,表达为F=qvB其中,F是洛伦兹力,q是带电粒子的电荷量,E是电场强度,v是带电粒子的速度,B是磁感应强度洛伦兹力定律是一个基本公理,不是从别的理论。
1845年,关于电磁现象的三个最基本的实验定律库仑定律1785年毕奥萨伐尔定律1820年法拉第电磁感应定律1831 ~ 1845年已被总结出来,法拉第的“电力线”和“磁力线”现在也叫做“电场线”与“磁感线”概念已发展成“电磁场概念”1855年至1865年,麦克斯韦在全面地审视了库仑定律;根据麦克斯韦第二个方程高斯磁定律 ,表明磁场的散度为零散度的大小可用于表征空间各点矢量场发散的强弱程度,当散度大于零,表示该点有散发通量的正源当散度小于零,表示该点有吸收通量的负源当散度等于零,表示该点为无源场高斯磁定律表明,磁单极子实际上并不存在于宇宙所以,没有磁荷;如图所示说明了磁场的来源有两个电流和变化的电场在麦克斯韦方程组中,电场和磁场已经成为一个不可分割的整体该方程组系统而完整地概括了电磁场的基本规律,并预言了电磁波的存在麦克斯韦提出的涡旋电场和位移电流假说的核心思想是变化的磁场可以激发涡旋电场,变化的电场可以激发涡旋磁场电场;3导体构成的电路若有中断处,电路中的传导电流将由电介质中的位移电流补偿贯通,即全电流连续且位移电流与其所产生的磁场的关系与传导电流的相同4磁通量既无始点又无终点,即不存在磁荷5光波也是电磁波麦克斯韦方程组是由四个微分方程构成1#8711·E=ρε0,描述了电场的。
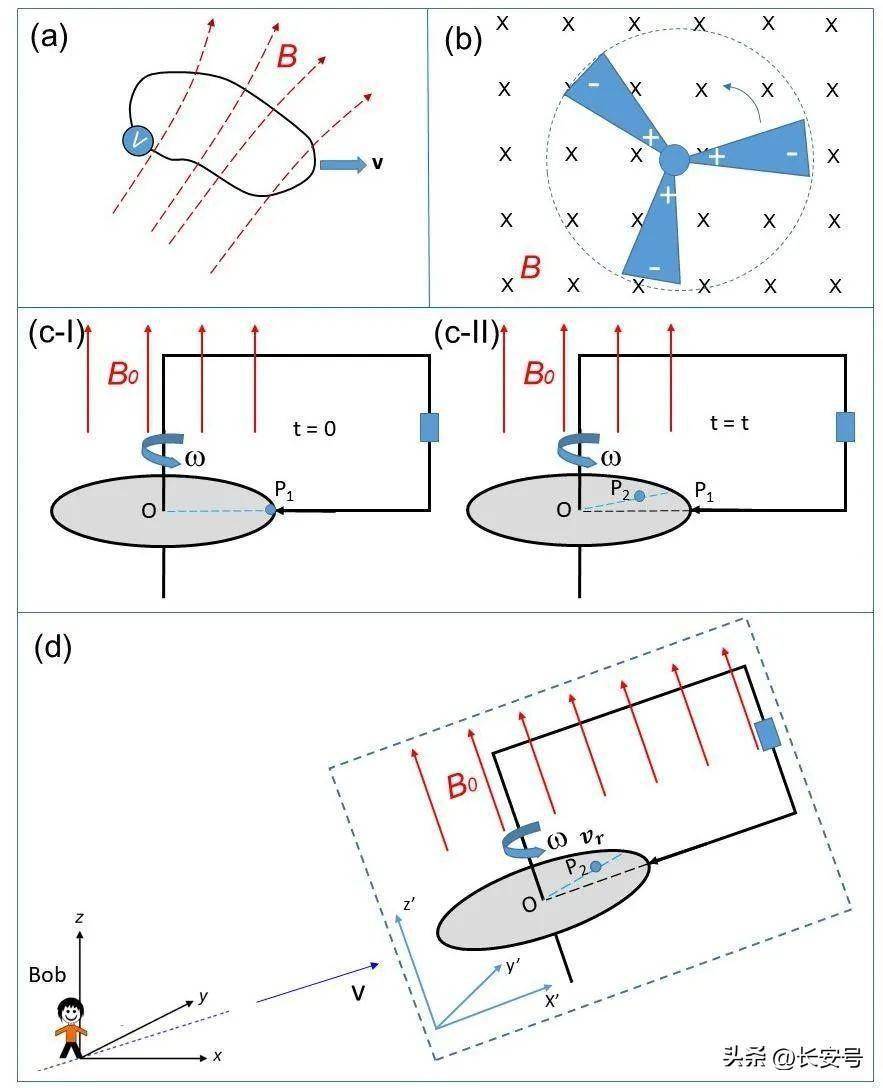
6磁力线总是从 N 极出发,进入与其最邻近的 S 极,并形成闭合回路这一现象在电磁学中称为磁通连续性定理,由 Maxwell 方程描述为· B =0 41上式又称为磁场的高斯定律,表示任意磁场的散度为 0 ,即通过任意闭合曲面的净磁通总是 0 ,磁力线总是闭合的同电流类似,磁力线总是走磁阻。