1、具体来说,设有一组数据点x_i, y_i,其中i=1,2n,以及一组对应的权重w_i我们的目标是找到一个函数fx,使得加权误差的平方和最小,即Sigmaw_i * y_i fx_i^2达到最小通过求解这个优化问题,我们可以得到最佳拟合函数以一个简单的线性回归为例,假设我们。
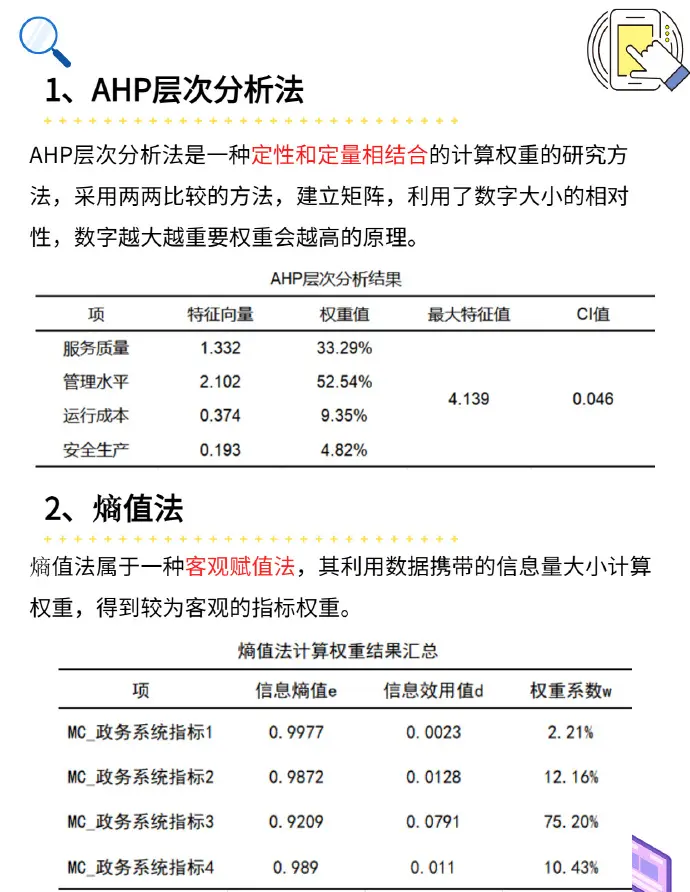
2、具体来说,加权最小二乘法会寻找一个模型参数集,使得带权重的误差平方和达到最小这个过程是通过迭代计算完成的,包括计算梯度更新参数等步骤最终得到的模型能够更好地反映数据的真实关系,并且在预测和决策中更为准确加权最小二乘法在许多领域都有广泛的应用,如金融分析物理建模生物信息学等。
3、一般来说,近期数据比起远期数据对未来的影响更大因此比较合理的方法就是使用加权的方法,对近期数据赋以较大的权数,对远期数据则赋以较小的权数加权最小二乘法采用指数权数Wni,0ltWlt1,加权以后求得的参数估计值应满足以直线模型 为例,其加权的剩余平方和为对上式分别求a和b的偏导数。
4、一般为误差平方和的形式,即Eβ=Σy_iβ_0β_1x_1iβ_2x_2iβ_n*x_ni^2,其中i表示第i个观测数据最小化残差函数将残差函数对参数进行求导,令导数等于0,求解出使残差函数最小化的参数估计值这可以通过解线性方程组矩阵运算或数值优化算法等方式实现参数估计与。
5、假设我们有n个观测数据点,每个点可以表示为xi, yi,其中xi是自变量,yi是因变量我们使用线性模型来描述这个关系,即yi = b0 + b1*xi其中,b1表示自变量xi的权重,我们可以通过最小化预测值与实际观测值之间的差异来估计这个权重在这个过程中,求和符号常用于计算误差平方和,以确定最佳拟合。
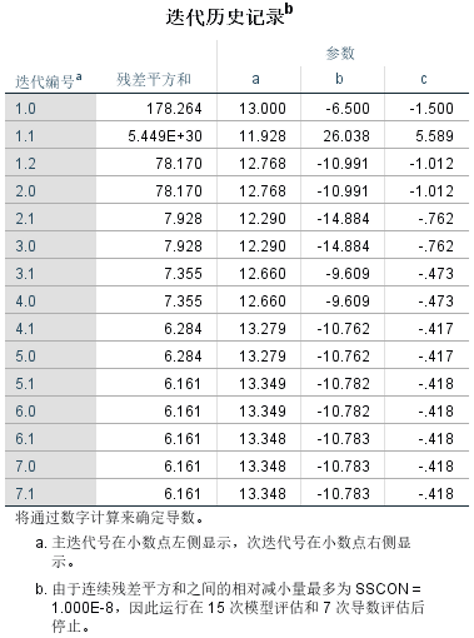
6、对于非等精度测量数据,残差平方和的公式则需考虑每个测量值的权重,即PV#178 = P1V1#178 + P2V2#178 + PnVn#178在这个公式中,PV#178代表加权残差平方和,而Pi则为相应的权重值,用于反映每个测量点的可靠性或精度残差是指实际观察值与估计值即拟合值之间的差异。
7、简单说就是求前n%数据的数量累加值和总数量总值,然后将前者相除再乘以后者即可得到赫芬达尔指数需要注意的是,Excel中的百分比计算可能会因为舍入误差而产生偏差,因此在计算时应该对结果进行适当的修正如果你已经把前50名的占有率放在A1A50,计算公式为 =SUMPRODUCTA1A50,A1A50 如果你。
8、平均数虽然容易受极端值的影响,但它能够充分利用所有数据的信息,而中位数和众数则更侧重于减少误差绝对值的和此外,基于数学证明,平均数能够使与数据差的平方和达到最小,即在代表数据时,平均数能使得二次损失最小算术平均数与加权平均数是两种常见的平均数计算方法算术平均数,即简单平均数。
9、BP算法,即误差反向传播算法,是由Rumelhart和McCelland在1986年提出的一种多层前馈网络训练方法它通过调整网络权重和阈值,使得网络的误差平方和最小BP网络能自动学习和存储大量输入输出模式映射关系,无需事先揭示这种映射关系的数学公式BP算法是一种监督学习算法,其主要步骤包括首先初始化网络权重。
10、xn是自变量,b0b1b2bn是回归系数,e是误差项在b估计方法中,首先计算出残差,然后通过最小化残差平方和,求解回归系数b具体来说,通过矩阵运算求解b=X#39^1*X#39WY,其中X为自变量的设计矩阵,Y为因变量的向量,W为权重矩阵,针对常见的回归问题,可以选择不同的权重矩阵。
11、3 最小平方平差法 最小平方平差法是一种该方法的目标是在满足约束条件的基础上,使每个方程的平方和之和最小化在这种情况下,未知质点可根据最小二乘法公式计算,因为当平方和最小化时,误差是最小的4 合同法平差方法 合同法平差法是一种基于建立基本的代数方程和通过消元法进行计算的平。
12、在实践中,MSE和RMSE常被用来比较不同模型的预测效果较低的MSE和RMSE值表明模型的预测更为准确然而,它们各自也有局限性MSE对异常值敏感,而RMSE则更能体现预测误差的大小,因为它使用了平方根操作在神经网络训练过程中,MSE和RMSE可以作为优化目标,通过调整网络权重来最小化它们这对于提高模型。
13、二公式及分析 最小二乘法的基本公式是用于线性回归的在简单线性回归中,我们试图拟合一个线性模型 y = mx + b 来最好地描述数据假设我们有 n 个数据点,表示为 x_i, y_i,其中 i 是数据点的索引我们的目标是找到最佳的斜率 m 和截距 b,使得拟合线与数据点的误差平方和最小。
14、权重衰减的基本思想是在损失函数中加入一个与权重相关的惩罚项这个惩罚项通常是所有权重的平方和乘以一个衰减系数通过最小化这个带惩罚项的损失函数,我们可以让模型在拟合训练数据的同时,保持权重的较小值,从而降低模型的复杂度,提高泛化能力以线性回归为例,假设我们的损失函数为均方误差MSE。
15、简单来说,就是在回归模型中,误差项的方差不是恒定的,而是与自变量相关异方差会给回归分析带来一些问题,例如,参数估计不准确假设检验失效预测区间不准确等因此,为了得到可靠的结果,需要采取一些方法来解决异方差问题解决异方差的方法1权重最小二乘法Weighted Least Squares,WLS权重。
16、首先,在Excel中输入数据,其中每行代表一个参与者,在同一列中输入其市场份额在另外一列中计算每个参与者的市场份额的平方对所有市场份额的平方进行求和,得到总和将每个参与者市场份额的平方除以总和,得到每个参与者的市场份额权重将所有参与者的市场份额权重相加,得到赫芬达尔指数公式为赫。
17、定理2BLUE的威力lt在列满秩的 Xlt 条件下,最小二乘估计是 βlt 的最好线性无偏估计BLUE,意味着没有其他线性估计方法能提供更低的均方误差对于 β_0lt 的估计,我们通常需通过非线性方法,因为其量纲限制了直接的线性估计于是,我们引入偏差平方和的概念,通过二次函数来逼近 β_0。