权重计算方法通常有因子分析或主成分分析AHP专家层次分析法熵值法CRITIC权重灰色关联法等等SPSSAU均有提供比如可以使用熵值法进行计算,具体操作如下熵值是不确定性的一种度量信息量越大,不确定性就越小,熵也就越小信息量越小,不确定性越大,熵也越大因而利用熵值携带的信;常用的方法包括层次分析法模糊法模糊层次分析法和专家评价法等2有题可以,授课老师的平均分=10+92=95 分 ,同学的平均分=10+82=9分根据权重分别是4321,可以计算出甲同学测评分数为9×04+95×03+9×02+9×01=915分;Sum_A=sumA%列求和n=sizeA,1%返回行数SUM_A=repmatSum_A,n,1 %弄成n*n矩阵Stand_A = A SUM_A对应的元素相除即可第二步将归一化的各列相加sumStand_A,2%按行求和第三步将相加后得到的向量中每个元素除以n即可得到权重向量disp‘算术平均法求权重;1权重计算即将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数2权重的值就是加权平均值,值的大小不仅取决于总体中各单位的数值变量值的大小,而且取决于各数值出现的次数频数,由于各数值出现的次数对其在平均数中的影响起着权衡轻重的作用,因此叫做权数。
权重的计算方法多种多样,最常见的是加权平均法加权平均法是指在计算平均值时,根据各个因素的权重来调整它们的贡献度比如,如果A因素的权重是2,B因素的权重是1,那么A和B的加权平均值就是A*2 + B*1 2+1这种计算方法可以更准确地反映出各个因素的相对重要性在实际应用中,权重;权重公式是一种计算方法,用于确定多个指标在整体评估中的相对重要性用数学表达式表示就是xweight = x1 * f1 + x2 * f2 + + xk * fk n,其中每个指标的权重f1, f2, , fk之和必须等于1,即f1 + f2 + + fk = n权重是一个相对值,它体现了某指标在综合。
层次分析法则是一种更为系统化的方法它通过构建一个层次结构模型,将复杂问题分解为若干层次和若干因素,然后量化分析各因素之间的关联和重要性这种方法能够综合考虑多种因素,得出相对客观的权重值熵权法则是基于信息熵理论来确定权重的方法信息熵反映了数据的不确定性,通过计算信息熵的数值,可以;01评分法的基本原理根据各功能因素重要性之间的关系,将各功能一一对比,重要者得1分,不重要的得0分为防止功能指数中出现零的情况,需要将各功能总得分分别加1进行修正后再计算其权重01评分法重要者得1分不重要者得0分自己与自己比较不得分,用叉号表示累计,用公式计算为;课程目标权重的计算方法因课程而异,但通常,首先根据课程教学大纲,将课程目标分解为与毕业要求指标点一一对应的课程分目标,并确定其权重,使得课程分目标权重总和为100%这些权重值的设定是基于课程教学大纲中的课程目标,不同的考核方式及其所对应的课程目标进行权重的设定,并由课程负责人和课程组老师讨。
1 权重计算是将每个值乘以相应的权重,然后求和得到整体值,再除以总单元数2 权值为加权平均值值的大小不仅取决于总体中每个单位变量值的值,还取决于每个值的次数频率因为每个值的次数在其对平均值的影响中起着平衡的作用,所以称其为权数;而在某些科研项目中,团队成员的贡献可能按照时间任务完成情况等因素分配不同的权重因此,权重计算方法灵活多变,适用于各种评价体系总之,权重的概念在评价体系中起着至关重要的作用通过合理设定权重,可以更加准确地反映各个指标的重要性,从而得出更为公正的评价结果。
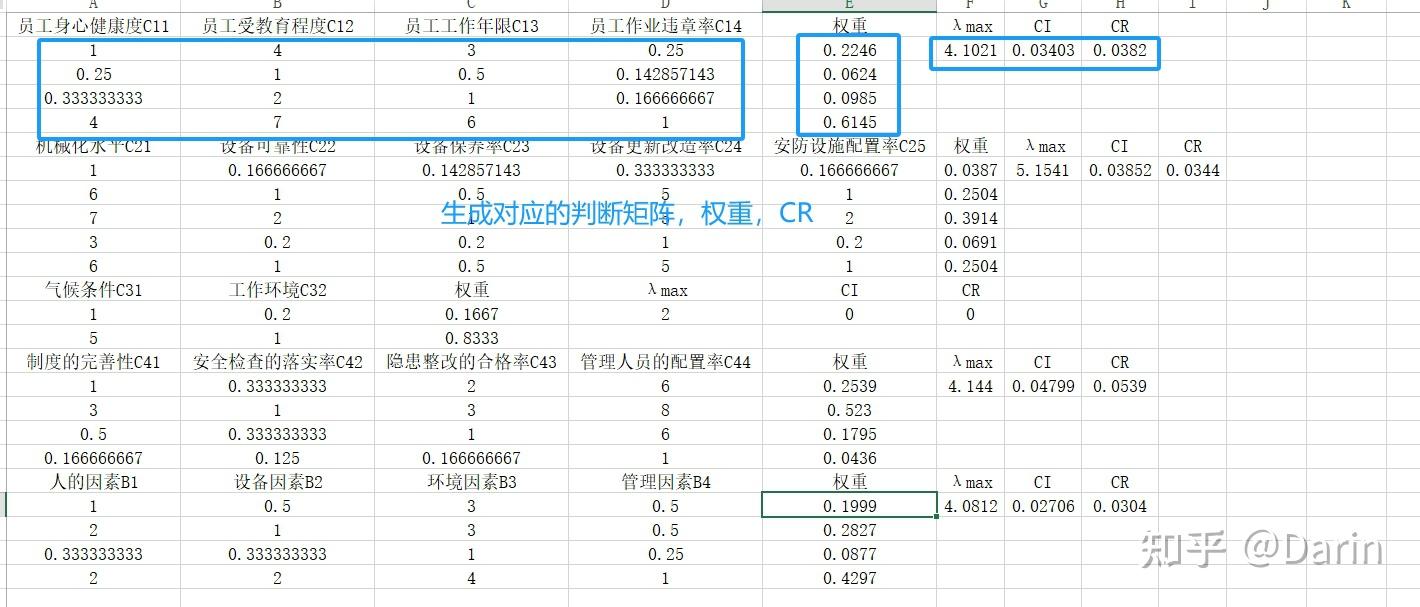
1 特征向量计算通过将判断矩阵一个由专家评分构成的矩阵,反映因素间相对重要性各列求和并进行归一化处理,得到特征向量特征向量表示各因素的相对权重2 权重值计算对归一化后的特征向量进行进一步处理,以得到各因素的具体权重值这些权重值表示各因素在决策中的相对重要性3 最大特征根。
在评估一个学生的综合成绩时,权重计算方法是一种常用且有效的方式以甲同学的测评为例,其分数由多个指标组成,如1 一项指标的得分是9,其权重为04,即9*04=362 第二项指标的得分是10+92=95,其权重为03,即95*03=2853 第三项指标的得分是9,其权重为0;权重得分的计算可以通过配对比较法来实现,具体步骤如下确定比较对象首先,明确所有需要计算权重的指标或刺激,这些指标将作为被比较的对象进行配对比较将所有待比较的指标一一配对,形成多个比较对一对一地呈现这些配对给评价者,要求评价者就每个配对中的两个指标在给定的某种属性上进行比较评价;计算权重系数的步骤权重系数是一种反映数据重要程度的数值在多变量分析中,通常用来反映某一因素对整体影响的相对程度以下是计算权重系数的方法一确定评价指标 首先,需要确定评价对象的具体指标这些指标应全面反映评价对象的各个方面例如,评价一个学生的综合素质,可以包括学习成绩课外活动。
