1521光滑粒子流体动力学Smoothed particle hydrodynamics,SPH适用产品AbaqusExplicit SPH是一种数值方法,属于无网格方法的一部分,不需要定义节点和单元,仅需一组点集表示体这些点称为粒子或伪粒子与传统有限元分析相比,SPH方法在没有边连接节点的情况下实现在“Finite elementconversion t;光滑粒子流体动力学SPH,一种拉格朗日观点的无网格方法,通过粒子离散形式探讨事物研究在特定领域中,SPH能解决相应问题,但允许意外发生,不意味着万能,却具有适用面SPH以伪粒子体现事物,这是它优势与劣势的来源在宏观层面,如船海领域,SPH通过光滑近似,以提高效率与实用性一个特殊函数。
蒙纳士大学在2020年QS世界大学排名中位列世界第58位,2019年泰晤士高等教育世界大学排名中位列世界第84名,2019年USNews世界大学排名中位列世界第62名,2018年世界大学学术排名中位列世界第91名蒙纳士大学有多个学科位列世界顶尖行列,其中药剂学与药理学专业常年位居亚太地区第一位,此外教育学护理学;物理学家费曼曾经说过,湍流可能是经典物理学中最后的一个未解难题NS 方程流体力学基石 流体力学的数值模拟对于建模多种物理现象而言非常重要,如天气气候空气动力学和等离子体物理学通常,流体可以用纳维 斯托克斯方程NavierStokes equations,NS来描述,但大规模求解这类方程仍属难题,受限。
2电磁场的动力学理论 1865年他发表了第四篇论文电磁场的动力学理论,为解决与光速之间的纯唯象问题提供了一个新的理论框架它以实验和几个普遍的动力学原理为根据,证明了不需要任何有关分子涡旋或电粒子之间的力的专门假设,电磁波在空间的传播就会发生3电磁专著电磁学通论 经过了八年的艰苦;光滑粒子流体动力学SPH是一种拉格朗日视角下的数值模拟方法,由Gingold和Monaghan等人提出,最初用于模拟星体相互作用问题随后,SPH方法扩展至计算流体力学计算固体力学及计算机图形学等多个领域在处理大变形高速度与自由液面流体时,SPH相较于有限体积法FVM等网格方法优势明显其中,DualSPHy。
光滑粒子流体动力学ansys
它能够精确描述质点的运动路径,常用于流体溯源分析 应用在Simversus的后处理模块中,迹线功能允许用户设置来源线粒子密度释放间隔等参数,并调整着色方式和不透明度以生成迹线用户可以通过播放动画,观察标量矢量动画与迹线生成的轨迹,为流体动力学方案提供数据支持若需单独查看迹线,可以关闭部件。
通过调节杠杆两端螺母使杠杆处于水位置的目的便于直接测定动力臂和阻力臂的长度 定滑轮相当于等臂5物理量符号及单位B磁感强度T,L有效长度m,I电流强度A,V带电粒子速度ms,q展开全部 力学是平衡态和相对作用,电学是电路分析和电磁学的电磁感应,热学得六态变化,浮力等。
杨米尔斯理论的存在性和质量缺口问题,则是物理学与数学结合的产物它涉及量子场论,探讨了基本粒子之间的相互作用解开这一难题,将有助于理解自然界的基本规律纳维叶斯托克斯方程的存在性与光滑性,是流体力学领域的一大挑战这一问题关乎于流体动力学的数学描述,寻找这些方程在所有情况下的解。
方程如下ax?D?+bxD+cy=fx只是其中一种形式,还有泛函极值条件的微分表达式等,这是属于无粘性流体动力学理想流体力学中最重要的基本方程,是指对无粘性流体微团应用牛顿第二定律得到的运动微分方程,它描述理想流体的运动规律奠定了理想流体力学基础 粘性流体是指粘性效应不可忽略的流体自然界中的。
杨-米尔斯存在性和质量缺口问题是物理学与数学之间的交叉难题,它涉及到规范场理论中的数学问题这个问题的解决将有助于物理学家更好地理解基本粒子的性质纳维叶-斯托克斯方程描述了流体动力学的基本规律,但其存在性和光滑性问题至今尚未解决这个问题的解决将对工程和物理学产生重大影响贝赫和斯维。
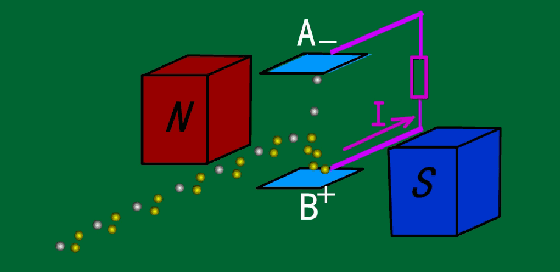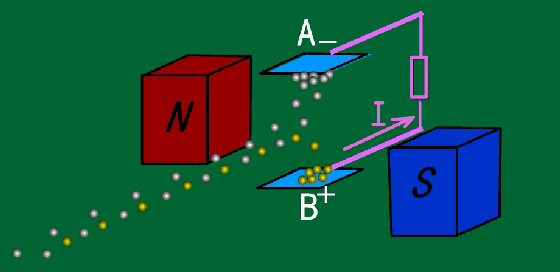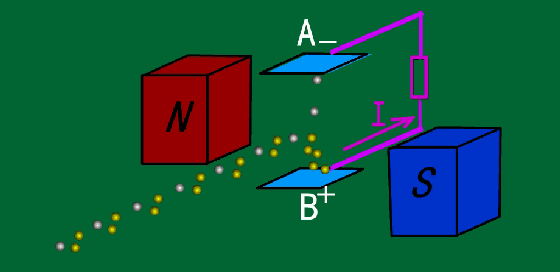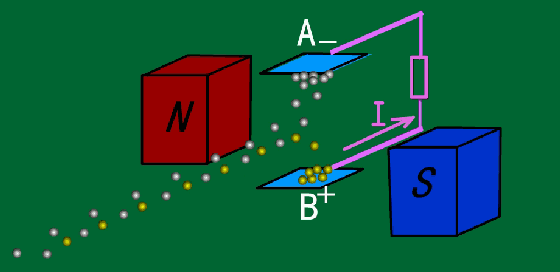
光滑粒子流体动力学缺点
莫纳什大学虽然整体排名不如墨尔本大学,但作为澳大利亚名校联盟“八大名校”之一,认可度是很高的蒙纳士大学Monash University,又译莫纳什大学,坐落于澳大利亚维多利亚州墨尔本,是一所蜚声国际的顶级公立研究型高等学府,世界百强名校,澳大利亚名校联盟“八大名校”之一,澳大利亚五星级大学,南半球首屈一指。

杨米尔斯存在性和质量缺口问题涉及量子场论和规范理论它探讨了杨米尔斯场的数学存在性以及质量间隙的存在性,这一问题对于理解基本粒子的性质至关重要纳维叶斯托克斯方程描述了流体运动的动力学,但其存在性和光滑性问题尚未解决这个问题的解决将有助于我们更好地理解流体动力学中的复杂现象,例如。
湍流有时形成一种有序的模式EPFL 虽然秩序往往会演变成混乱,但有时恰恰相反例如,湍流流体有一种自发形成整齐图案的趋势平行条纹虽然物理学家已经通过实验观察到了这种现象,但他们现在可以用基本流体动力学方程解释为什么会发生这种情况,使他们更接近理解粒子为什么会以这种方式运动物理学中最。
高级有限元无网格粒子法用于解决固体材料大变形和破坏行为的分析难题,包括光滑粒子伽辽金法SPG键型近场动力学法Bondbased Peridynamics和扩展有限元法XFEM电磁EM Solver结合有限元法FEM和边界元法BEM,为用户提供稳定可扩展精确的电磁过程模拟电器求解器与结构热和流体的强。
光滑粒子流体动力学方法SPH Smoothed Particle Hydrodynamics是近20多年来逐步发展起来的一种无网格方法,该方法的基本思想是将连续的流体或固体用相互作用的质点组来描述,各个物质点上承载各种物理量,包括质量速度等,通过求解质点组的动力学方程和跟踪每个质点的运动轨道,求得整个系统的力学行为。