1、决策变量直接关系到利润的多少目标条件多个决策变量的线性函数,通常是求最大值或最小值问题约束条件一组多个决策变量的线性等式或不等式组成线性规划建立的数学模型具有以下特点1每个模型都有若干个决策变量x1,x2,x3,xn,其中n为决策变量个数决策变量的一组值表示一种方案。
2、决策变量是指最优化问题中所涉及的与约束条件和目标函数有关的待确定的量一般来说,它们都有一些限制条件约束条件,与目标函数紧密关联。
3、2目标函数希望最大化或最小化的目标,当在一个生产问题中,目标是最大化利润,即最大化总收入减去总成本3约束条件这些条件描述了哪些决策变量的取值是允许的,以及两者之间的关系,在一个生产问题中,约束条件包括设备的使用时间限制,以及某些决策变量的取值范围。
4、决策变量目标函数问题是运筹学中的一个重要问题,它涉及到在给定约束条件下,如何确定最优的决策变量值以实现特定的目标分析这类问题通常需要遵循以下步骤1确定目标函数首先,我们需要明确我们希望优化的目标这个目标通常用一个数学函数来表示,称为目标函数目标函数可以是线性的或非线性的,取决。

5、决策变量x和y可以分别代表这两种产品的生产数量目标函数可能是每种产品的利润与其生产数量的乘积之和,形如5x + 7y同时,制造商可能面临原材料劳动力或生产时间的限制,这些限制可以通过线性不等式或等式来表示,如2x + 3y le 100在这个例子中,线性规划将帮助制造商找到在满足所有约束条件的。
6、变量或决策变量定义线性规划问题中涉及的一系列未知量,这些未知量代表决策方案中的具体数值特点这些变量在问题中通常以线性形式出现,即它们的系数是常数,且变量之间不存在非线性关系目标函数定义线性规划问题中需要最大化或最小化的函数,它通常是由决策变量的线性组合构成的特点目标。
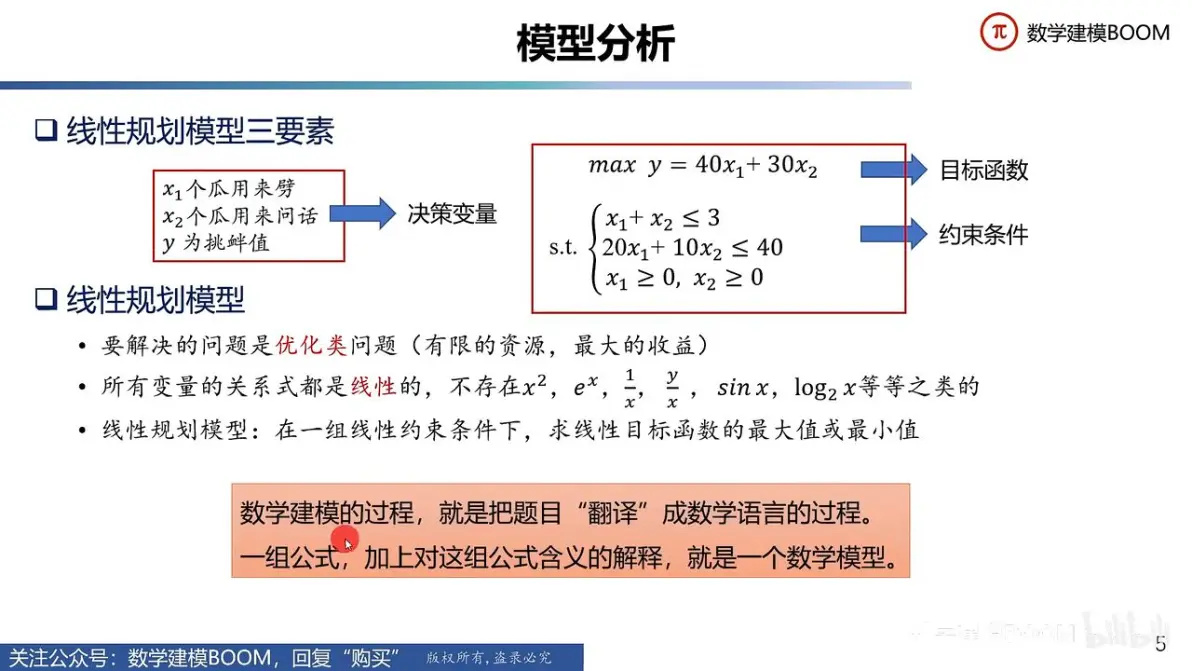
7、一般来说,一个优化模型将由以下三部分组成 1 目标函数Objective Function 要达到的目标 2 决策变量Decision variables 每组决策变量的值代表一种方案在优化模型中需要确定决策变量的最优值,优化的目标就是找到决策变量的最优值使得目标函数取得最优 3 约束条件。
8、决策变量代表需要求解的未知量,一般以n维向量表示,其中xj是问题中的第j个决策变量当赋予变量特定值时,即为问题的一个解目标函数则表示需要优化的指标,通常为决策变量的函数,用于衡量问题的最优性约束条件则限制决策变量的取值范围,这些条件可以通过等式和不等式来表达,形成可行域数学规划模型。
9、这意味着目标函数可以表示为决策变量的加权和,且加权系数即系数为常数例如,目标函数可以写成z = c1*x1 + c2*x2 + + cn*xn的形式,其中c1, c2, , cn是常数,x1, x2, , xn是决策变量求最大值或最小值线性规划模型的目标通常是求目标函数的最大值或最小值约束条件的线性性线性等式或不等式。
10、建立目标函数根据优化目标,用决策变量的函数表示出来,并确定是求极大值还是极小值明确约束条件列出所有对决策变量取值范围或关系的限制条件,并用数学语言表示研究变量的非负性根据变量的物理性质,判断其是否具有非负性,这有助于进一步缩小优化范围三优化问题的求解方法 传统优化方法对于。
11、是指在决策过程中,决策者可以控制和影响的数量或因素具体数值决定了某个具体的决策方案,通过对这些变量的设定和调整,决策者可以实现对决策结果的操控和优化决策变量可以是实际的问题相关的因素,例如产品的产量物资的运量或工作的天数等在数学模型中,决策变量通常作为目标函数的自变量决策变量的。
12、3约束条件每一个问题都有一定的限制条件,这些条件称为约束条件它是用一组线性等式或不等式来表示的,其变量与目标函数变量必须是有机联系或者一致的因为目标函数和约束方程都是决策变量的线性表达式,所以这类模型称为线性规划模型线性规划的数学模型可表示为目标函数 华北煤田排水供水环保。
13、组成要素决策变量代表需要决策的量,可以是连续的或离散的目标函数表示需要优化的量,是决策变量的函数约束条件对决策变量的取值范围或相互关系的限制,确保方案在实际中是可行的类型线性规划目标函数和约束条件都是决策变量的线性函数在线性规划中,可行域是凸集,最优解通常位于凸集的。
14、从实际问题中建立数学模型一般有以下三个步骤1根据影响所要达到目的的因素找到决策变量2由决策变量和所在达到目的之间的函数关系确定目标函数3由决策变量所受的限制条件确定决策变量所要满足的约束条件每个模型都有若干个决策变量x1,x2,x3,xn,其中n为决策变量个数决策变量的。
15、优化问题通常由决策变量目标函数和约束条件三部分组成决策变量需要作出的决策,如原材料的订购时间地点,生产计划的制定,产品的交付时间和数量等目标函数经济上或其他方面所要达到的目标,如利润最大化供应链成本最低化生命周期最短化客户服务质量最高化延误最短化产量最大化以及。
16、这个时期,通过GB丹齐克提出的单纯形法基础,发展出了针对可分离规划和二次规划的多种解法50年代末至60年代,众多有效算法应运而生,70年代则继续取得技术进步在实际问题的数学建模中,非线性规划起着关键作用首先,需要确定目标变量和决策变量,构建目标函数,它是目标变量与决策变量之间函数关系。