决策树生成根据特征筛选准则,选择数据集信息增益最大的特征进行分裂,直到所有叶节点的不确定性为0决策树剪枝通过决策树剪枝,得到不同的正则化参数α下的最优决策树模型剪枝步骤包括将正则化参数α从小到大分成不同的区间,对决策树的非叶节点进行剪枝,当α满足一定条件时,对该节点进行剪枝测试阶段 通过测试集评估。
输入训练数据集首先,输入包含连续数值型特征的训练数据集选择最优特征与切分点从数据集中选择最优特征和最优切分点,将节点数据集划分为两部分,并为这两部分分配相应的输出值递归划分对每个子集重复执行上述过程,直至满足特定的停止条件生成回归树最终生成一棵回归树,其中叶子节点的值作为。
具体过程自下而上计算每个内部节点的误差增加率即剪枝前后损失函数的变化量,选择误差增加率最小的节点进行剪枝,生成新的树如果新的树不是由根节点和两个叶节点构成的树,则递归上一步采用交叉验证法在上述两步中选择最优的子树作为最后的结果总结 CART算法是一种强大的决策树算法,既可以。
在剪枝过程中,通过计算剪枝前后损失函数的变化来决定是否剪枝具体步骤包括从决策树根节点开始,对每个内部节点计算损失函数变化量,选择损失函数减少幅度最大的节点进行剪枝通过不断剪枝并测试不同剪枝阈值下的决策树性能,选择使得验证数据集上性能最优如平方误差或基尼指数最小的决策树作为最终模型。
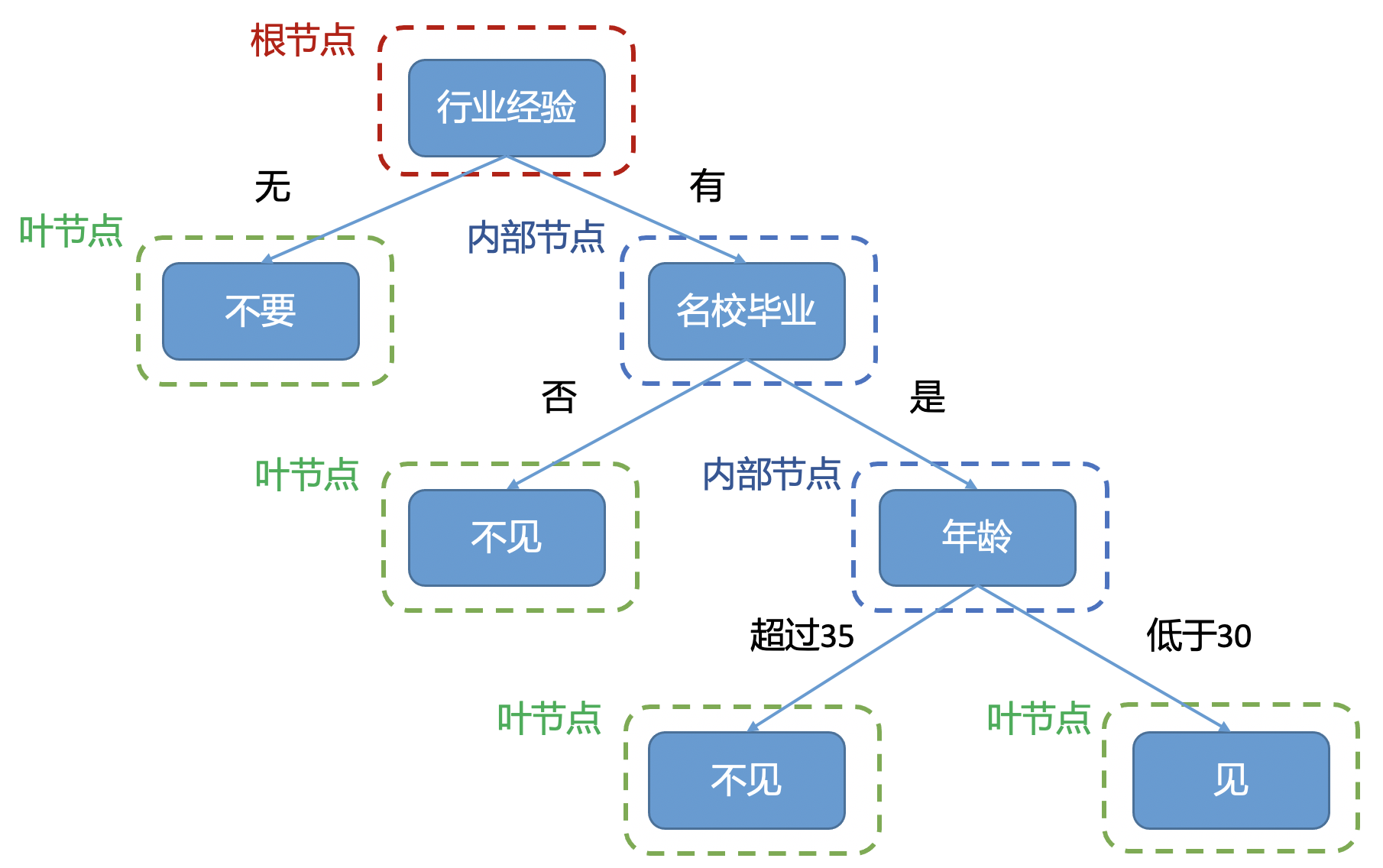
决策树法的步骤1 收集数据并预处理2 选择决策树的算法3 构建决策树模型4 评估和优化决策树模型5 应用决策树模型进行预测或分类接下来进行 1 收集数据并预处理在这一步中,需要收集与问题相关的数据,并对数据进行清洗和预处理,以便输入到决策树模型中数据预处理包括数据清理。
利用 ID3 算法构建决策树是一种有效的方法,尤其在面对复杂决策时首先,从信息量最大的条件开始推断结果,能够以最少的步骤达到目的在构建决策树时,通过量化信息量,使用信息熵作为度量工具,来选择最佳分叉点信息熵定义为集合中正反例的比例,通过公式 EntropyS = p+log2p+ plog2。
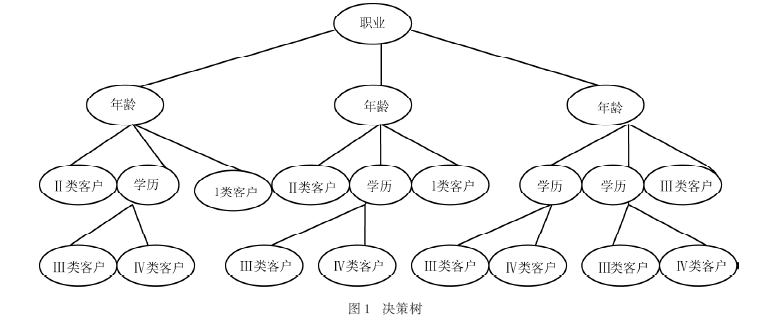
根据这三个步骤,可以确定决策树由1特征选择2生成方法3剪枝,组成 决策树中学习算法与特征选择的关系如下图所示原始特征集合T就是包含收集到的原始数据所有的特征,例如麻瓜银行收集到与是否具有偿还能力的所有特征,如是否结婚是否拥有100w的房产是否拥有汽车是否有。
二决策树的原理决策树的学习过程旨在生成一棵泛化能力强的树,通常分为以下三步特征选择筛选出跟分类结果相关性较高的特征,即分类能力较强的特征在特征选择中,通常使用信息增益作为准则决策树生成从根节点出发,对节点计算所有特征的信息增益,选择信息增益最大的特征作为节点特征,并根据该。
决策树的生成算法分为两个步骤预剪枝和后剪枝#160 CCPcost and complexity算法在树变小和变大的的情况有个判断标准误差率增益值α值为误差的变化 决策树的终止条件#160 #160 #160 1,某一个节点的分支所覆盖的样本都是同一类的时候 #160 #160 #160 2,某。
算法理论我了解的决策树算法,主要有三种,最早期的ID3,再到后来的C45和CART这三种算法这三种算法的大致框架近似决策树的学习过程 1特征选择 在训练数据中 众多X中选择一个特征作为当前节点分裂的标准如何选择特征有着很多不同量化评估标准,从而衍生出不同的决策树算法2决策树生成 根据选择的特征评估标准,从上至下递归生成。
三决策树构建过程 数据预处理清洗数据,去除缺失值和异常值将分类变量如是否拥有学生身份是否对电脑有兴趣进行编码,转换为数值形式特征选择选择对预测目标有显著影响的特征,如年龄收入学生身份电脑兴趣等构建决策树使用递归的方式构建决策树,每次选择最优的特征进行划分,直到。
ID3算法的工作流程数据准备算法要求数据是离散的,且类别明确样本数量需要足够多以区分真实模式和随机现象属性选择通过计算每个属性的信息增益,选择增益最高的属性作为划分依据决策树生成递归地应用上述过程,直到满足停止条件ID3算法的变种非递归ID3从固定训练数据中推导出分类规则增量。
C45算法有如下优点产生的分类规则易于理解,准确率较高其缺点是在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效此外,C45只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时程序无法运行具体算法步骤如下1创建节点N2如果训练集为空,在返回节点N。
暂无 请你用下面的例子来模拟下决策树的流程,假设好苹果的数据如下,请用 ID3 算法来给出好苹果的决策树红的信息增益为1大的信息增益为0 因此选择红的作为根节点,大没有用,剪枝数据分析实战45讲17 ,决策树上要不要去打篮球决策树来告诉你。
多叉树ID3的内部结点是属性,边是该属性的所有取值,有几个属性值就有几条边树的叶子节点都是类别标记由于数据表示不当有噪声或者由于决策树生成时产生重复的子树等原因,都会造成产生的决策树过大因此,简化决策树是一个不可缺少的环节寻找一棵最优决策树,主要应解决以下3个最优化问题。