1、权函数的选择有配置法矩量法最小二乘法和伽辽金法,后者尤其将权函数设置为逼近函数的基函数最小二乘法则是通过使权函数等于余量,以达到平方误差最小化配置法则通过在特定配置点上确保微分方程的满足来构造近似解插值函数的类型多样,包括线性高次多项式,甚至三角函数或指数函数的乘积常;最小二乘估计是一种普遍运用的统计估计方法,尤其在处理线性模型时我们首先探讨GaussMarkov模型的定义和基本性质模型表述为 其中X为n×p的观测向量,β为未知p维参数向量,ε为n维随机误差向量,与X正交且Eε=0,Varε=σ^2I在这一模型下,最小二乘估计定义为使残差平方和最小的参数。
2、线性最小二乘法基于线性模型,目标是找到一组回归系数,使得预测值与实际值之间的差最小普通最小二乘法假设残差均值为零加权最小二乘法允许不同观测值具有不同的权重,以反映其相对重要性或准确度非线性最小二乘法用于处理非线性模型的情况重要性最小二乘法是数据科学和统计分析中;最小二乘法是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小最小二乘法还可用于曲线拟合其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达最小二乘法;关于广义加权最小二乘法,加权最小二乘法这个很多人还不知道,今天来为大家解答以上的问题,现在让我们一起来看看吧1最小二乘法是一种数学优化技术,它通过最小化误差的平方和找到一组数据的最佳函数匹配2最小二乘法是用最简的方法求得一些绝对不可知的真值,而令误差平方之和为最小3;最小二乘法原理简单来说就是一种找最佳匹配的方法最小化误差平方和它就像是一个超级细心的数学家,会仔细计算每个观测值与通过某个函数预测的值之间的误差,然后加起来求平方,目标是让这个平方和变得尽可能小这样,它就能找到一个函数,这个函数能最好地“拟合”或匹配你的数据啦求定最可靠;加权最小二乘法是处理异方差性的一种有效方法以下是关于WLS的要点定义与原理定义加权最小二乘法是最小二乘法的扩展,通过赋予观测值不同的权重来处理异方差问题原理在OLS中,所有观测值的权重是相同的然而,在WLS中,权重是根据误差方差来确定的,特别是当误差方差在不同观测值之间不;三阶,四阶还能算,如果一百阶呢,所以用迭代最小二乘,迭代最小二乘是通过矩阵引理来计算,就是说比如原来有三个数据 用最小二乘法算出所求的系数矩阵,如果再来一个数据变成四个数据的时候,前三个不动然后通过矩阵原理算出新的所求系数矩阵;如果是一般的回归,那么加权最小二乘法取权仅仅是方程本身误差项的绝对值的倒数两种方法1蠢且勤快的方法在回归结果窗口中按Estimate,改变你的回归项分别为“y*1absresid x1*1absresid x2*1absresid”,当然要在做完你的OLS后马上做,否则你的resid序列就不是你所要的误;异方差加权最小二乘法的权数是1x2的原因在样本容量足够的情况下,尝试用White检验找出英气异方差的解释变量,用Glejser检验找出残差e随该解释变量变化而变化的函数形式,以该函数开方的倒数进行加权最小二乘法估计加权变换可以消除异方差性,使随机误差项变成同方差的这样才会满足线性回归模型的经典;加权最小二乘法的概念 加权最小二乘法是一种数学优化技术,用于处理数据拟合和函数逼近问题在统计学和数据分析中,它常用于处理存在噪声或误差的数据集,通过最小化加权误差的平方和来寻找最佳的函数匹配这种方法能够考虑到数据点的重要性或可靠性,通过为每个数据点分配权重来优化拟合过程加权最小。
3、1 求根 二分法牛顿法简单迭代法 牛顿法 迭代公式公式FX的雅克比矩阵 公式2 最小二乘拟合 最小二乘拟合是将包含统计不确定性的数据拟合为公式“理论”的首选方法公式已知数据点xi, yi,在函数空间公式中寻找S*xi,使得 公式其中公式是点xi处的权 在连续;定理2BLUE的威力lt在列满秩的 Xlt 条件下,最小二乘估计是 βlt 的最好线性无偏估计BLUE,意味着没有其他线性估计方法能提供更低的均方误差对于 β_0lt 的估计,我们通常需通过非线性方法,因为其量纲限制了直接的线性估计于是,我们引入偏差平方和的概念,通过二次函数来逼近 β_0。
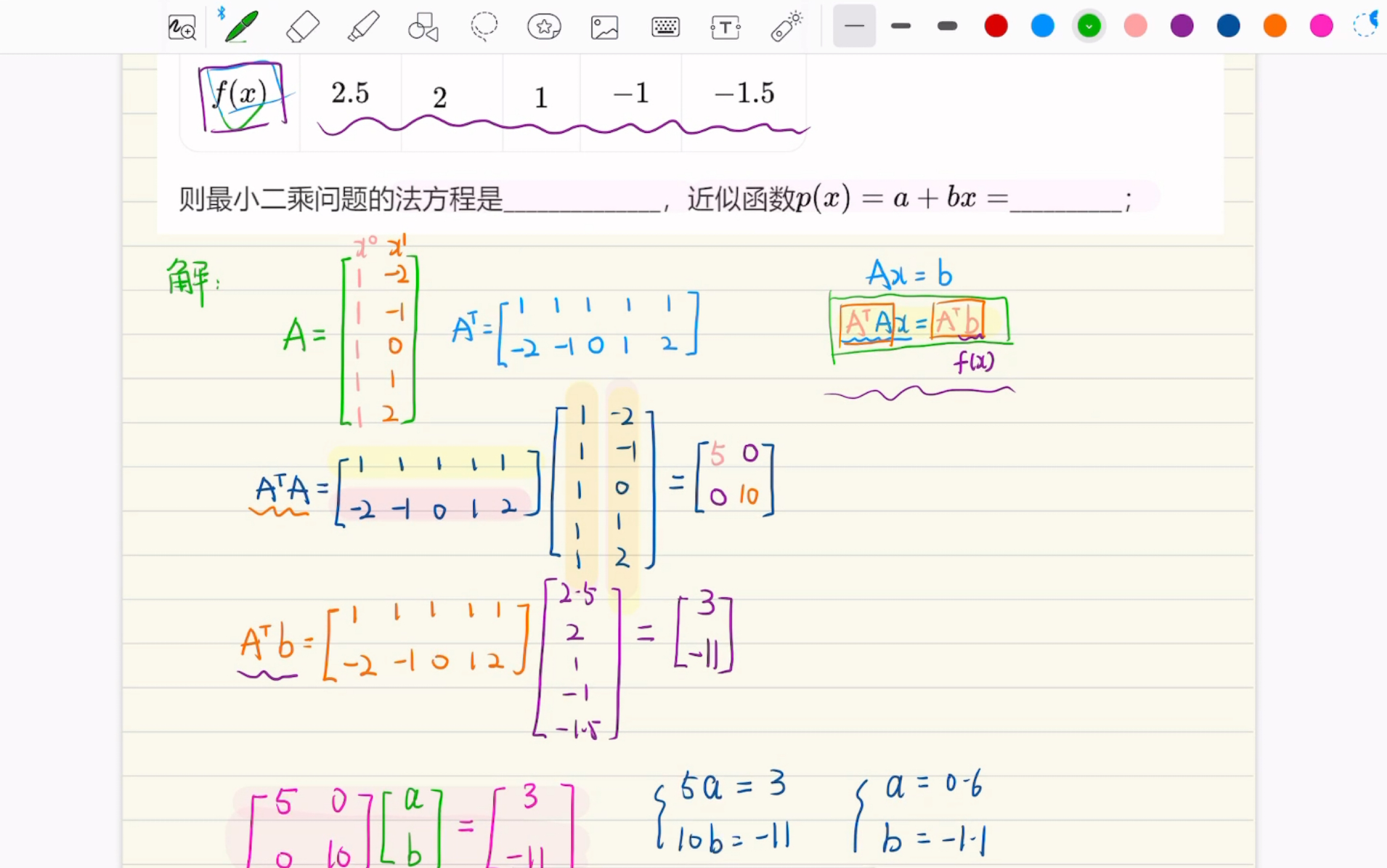
4、勒让德和高斯发现最小二乘法是从不同的角度入手的一个是为解线性方程组,一个是寻找误差函数一个用的是整体思维,考虑方程组的均衡性,一个用的是逆向思维,首先接受经验事实一个是纯代数方法,一个致力于应用再回到开头的问题按照最小二乘原理的要求,认为“最佳”地拟合于各观测点的;最小二乘法公式是一个数学的公式,在数学上称为曲线拟合,此处所讲最小二乘法,专指线性回归方程最小二乘法公式为a=y平均b*x平均最小二乘法又称最小平方法是一种数学优化技术它通过最小化误差的平方和寻找数据的最佳函数匹配利用最小二乘法可以简便地求得未知的数据,并使;加权最小二乘法在数据拟合过程中,考虑到不同数据点的权重差异,对残差函数进行加权处理非线性最小二乘法将最小二乘法推广到非线性模型问题,通过迭代优化算法求解参数估计值鲁棒最小二乘法考虑到异常值对结果的影响,通过引入鲁棒估计方法,提高对异常值的抗干扰能力关于lg的应用 数据拟合。
