1递归的基本概念程序调用自身的编程技巧称为递归,是函数自己调用自己一个函数在其定义中直接或间接调用自身的一种方法,它通常把一个大型的复杂的问题转化为一个与原问题相似的规模较小的问题来解决,可以极大的减少代码量递归的能力在于用有限的语句来定义对象的无限集合2迭代利用变量的原值推算。
2递归法在计算机编程中,一个函数在定义或说明中直接或间接调用自身的编程技巧称为递归通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量递归做为一种算法在程序设计语言中广。
递归是一种编程技巧,指的是函数自我调用的过程通过函数的自我调用,可以将一个大问题分解为更小规模的同类问题,逐步解决这些子问题,最终达到解决原问题的目的例如,计算阶乘计算斐波那契数列等问题常使用递归方法递归的实现方式在实现递归函数时,需要明确函数的递归关系和基本情况以计算阶乘为。
递归是编程中一个关键的概念,它指一个函数通过在其内部调用自身来解决问题具体来说工作原理递归函数会反复调用自身,直到达到一个基本情况,然后逐层返回结果以计算阶乘为例,一个递归函数会先调用自身来计算较小数的阶乘,直到达到0的阶乘,然后逐层返回并计算结果特点递归与迭代密切相关,但。
A“递归”源自于数学上的递推式和数学归纳法B“递归”与递推式一样,都是自递推基础计算起,由前项第n1项计算后项第n项,直至最终结果的获得C“递归”是自后项即第n项向前项第n1项代入,直到递归基础获取结果,再从前项计算后项获取结果,直至最终结果的获得 D“递归。
递推与递归是计算机编程中两种重要的算法概念它们之间的区别在于过程方向和实现方式递推是从已知情况出发,通过重复应用某个规则或公式,逐步逼近目标结果它是一种从“已知到未知”,“从小到达”的计算方式,比如每年身高增长9cm,20年后身高为180cm,30年后为270cm递归则是从目标结果出发,反向。
递归是一种编程中的概念,指的是一种自我调用的过程详细解释如下递归的基本含义 在计算机科学中,递归是一种解决问题的方法,它通过不断地调用自身来解决问题的一部分,直至达到解决问题的最终答案或边界条件这个过程通常是处理可分割且层级化的任务的有效方式递归的基本原理 递归通常涉及两个关键。
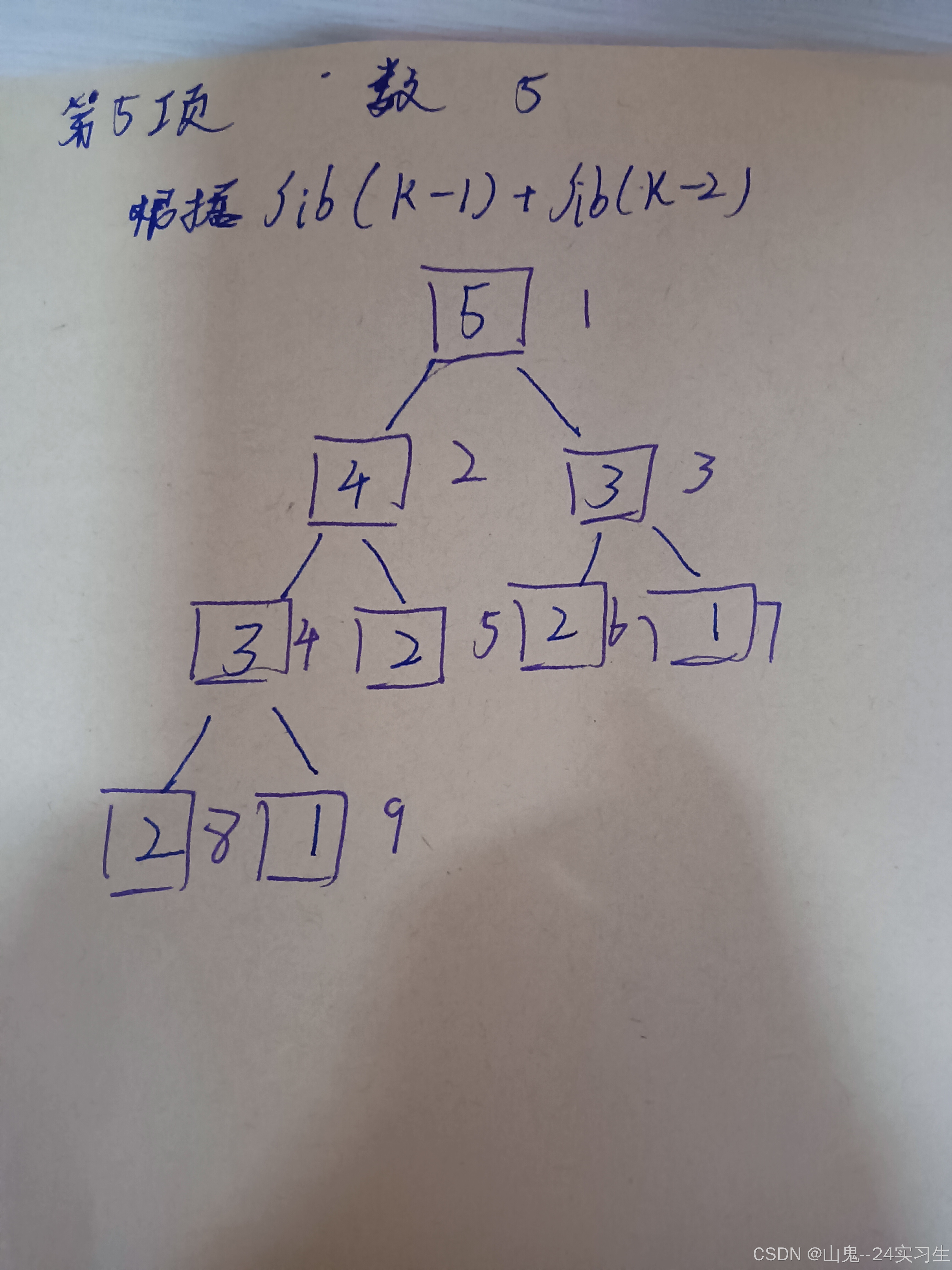
一般来说,递归需要有边界条件递归前进段和递归返回段当边界条件不满足时,递归前进当边界条件满足时,递归返回递归一般的作用用于解决三类问题1数据的定义是按递归定义的Fibonacci函数2问题解法按递归算法实现这类问题虽则本身没有明显的递归结构,但用递归求解比迭代求解更简单,如。
1递归是一种重要的编程思想,它指的是在函数的定义中调用函数自身的方法递归函数的特点是在函数内部调用自身,并且每次调用都会解决一个小问题,从而最终解决原始问题递归函数可以分为两个部分基准情况base case和递归规则recursive rule2基准情况是指递归函数可以直接返回的情况,而递归。
递归是指在函数或过程或子程序在运行过程中直接或间接调用自身而产生的重入现象在计算机编程中的具体定义和特点如下定义递归指的是一个过程或函数在其执行过程中不断引用自身,直到达到某个已知条件或基准情况为止特点自我引用递归函数在解决问题的过程中,会调用自身来解决子问题基准情况。
递归定义是一种在数学和计算机科学中用来定义函数关系对象或其他数学结构的方法,它基于对象自身的定义,即一个定义依赖于自身的一部分来展开递归定义通常包含以下关键部分1 基础情况Base Case定义起点基础情况是递归定义的起点,它描述了当输入达到某种特定值时,对象如何直接被定义这是。
递归就是一个函数在它的函数体内调用它自身执行递归函数将反复调用其自身,每调用一次就进入新的一层递归函数必须有结束条件当函数在一直递推,直到遇到墙后返回,这个墙就是结束条件所以递归要有两个要素,结束条件与递推关系递归有两个基本要素1边界条件确定递归到何时终止,也称为。
1 递归就是程序调用自身的编程技巧它像一个聪明的孩子,在解决复杂问题时,会先尝试把大问题拆分成小问题,然后用同样的方法去解决这些小问题,直到问题变得非常简单,可以直接解决2 递归的作用可大了去了第一,它能帮我们解决那些按递归定义的数据问题,比如著名的Fibonacci数列,就是每个数是。
递归是一种编程技巧,指的是程序在执行过程中调用自身的方法,以解决复杂问题的一种策略以下是关于递归的详细解释核心思想递归的核心思想是将大问题分解为规模较小的相似问题,通过重复计算逐步逼近答案优势简洁性递归允许程序员用简洁的代码描述多次重复的过程,从而大大减少了代码量效率。
递归函数的基本思想如下递归就是方法自己调用自己 递归特点 有临界点 当一个方法执行完毕,或者遇到retrun,就会返回,函数就是出栈待求解问题的解 输入变量x的函数fx,通过寻找函数g , 使得fx = gfx1且已知f0的值, 就可以通过f0和g 求出fx的值扩展到多个。
递归函数是指一种特殊类型的函数,它会在其定义或实现中调用自身递归是一种强大的编程技术,用于解决可以分解为更小的相似问题的问题在递归函数中,通常会有一个或多个基本情况base cases,这些是函数可以直接求解而无需进一步递归的情况此外,还需要有递归情况recursive cases,在这些情况下。

递归是一种编程技术,其中函数直接或间接地调用自身,以解决一个复杂问题,将其分解为更小的子问题递归的核心在于定义一个函数,该函数通过调用自身来解决规模较小的问题,直到达到一个基本情况,此时不再进行递归调用递归的正确使用需要确保存在一个终止条件,否则会导致无限递归,消耗大量资源例如。
递归算法包含的两个部分1由其自身定义的与原始问题类似的更小规模的子问题只有数据规模不同,它使递归过程持续进行,称为一般条件2所描述问题的最简单的情况,它是一个能控制递归过程结束的条件,称为基本条件递归出口递归的定义如果一个对象部分地由它自身组成或按它自己定义,则。