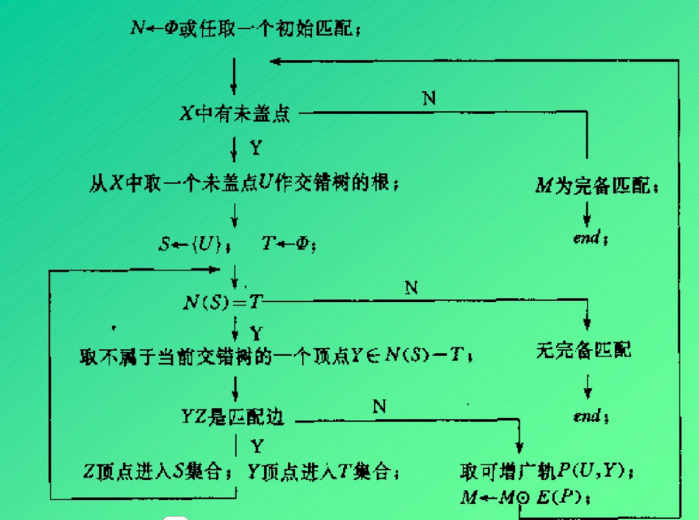
K#337nig 定理揭示了在二部图中,最大匹配数与最小点覆盖数之间的等价关系即在任意二部图中,最大匹配数等于最小点覆盖数直观理解,最大匹配意味着在图中尽可能多地将顶点配对,而最小点覆盖则意味着在不破坏这些匹配的情况下,最少需要选择多少顶点定理指出这两者在数值上相等,提供了求。
模型参数迭代本质上是二部图中的最大带权匹配问题可以将商品item和叶子节点leaf视为节点,索引结构为连接item和leaf的边,目标是根据损失函数中设置的边权重计算方式,选择合适的索引结构最大化所有商品的连接权重针对这个问题,传统的Hungarian算法或naive greedy算法由于计算复杂度和存储复杂度的限制。
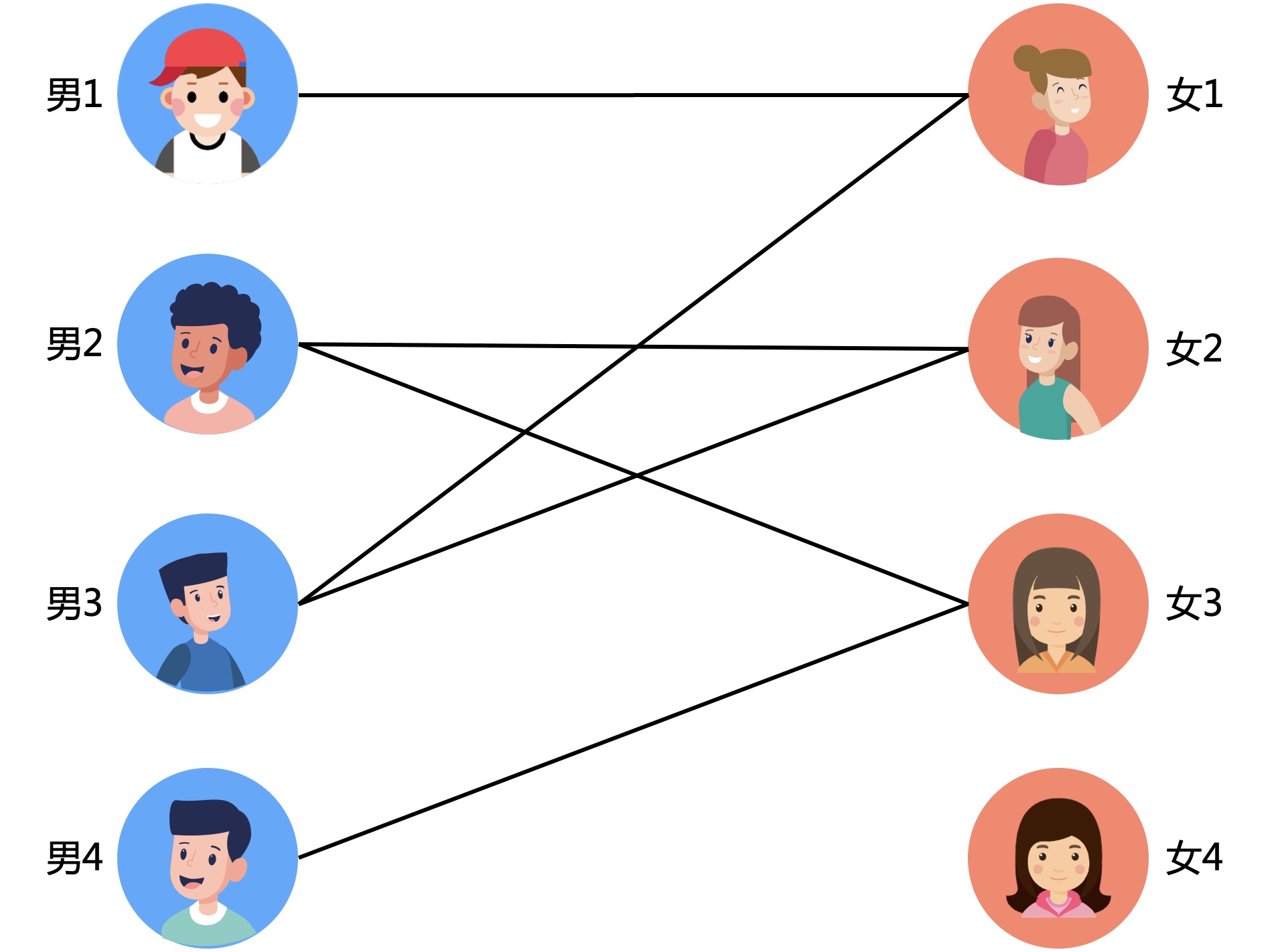
KM算法的正确性基于以下定理若由二分图中所有满足A i +Bj=wi,j的边i,j构成的子图称做相等子图有完备匹配,那么这个完备匹配就是二分图的最大权匹配首先解释下什么是完备匹配,所谓的完备匹配就是在二部图中,X点集中的所有点都有对应的匹配且Y点集中所有的点都有对应的。
#160 #160 #160 #160 第六章为特殊的图,主要讲了主要讲了二部图,欧拉图,哈密顿图和平面图#160 #160 #160 #160 第一节为二部图,介绍风格和往常一样,先介绍了很多概念,比如二部图偶图,互补顶点子集,和一些匹配的相关概念,大面上来说,二部图就是能把。
三索引迭代 最大带权匹配问题模型参数迭代本质上是二部图中的最大带权匹配问题,目标是选择合适的索引结构最大化所有商品的连接权重 算法复杂度限制传统的Hungarian算法或naive greedy算法由于计算复杂度和存储复杂度的限制,难以在大规模工业场景中实施四分割树学习算法 逐步确定索引结构分割。
公式包含公式,且仍是简单图因为G的最大度点在公式中已经是公式度的,所以这些点在公式中的邻点不变,添上M后不会有重边2 通过1证明即可,注意无环边意味着可通过去掉G的一些边使其变为二部图66 将公式划分为公式个不交匹配,每个匹配至多公式条边。
1匹配不同V1中每个顶点至少关联tt0条边,V2中每个顶点至多关联t条边,则G中存在V1到V2的完备匹配2条件不同Hall定理中的条件为相异性条件,满足t条件的二部图,一定满足相异性条件,事实上V1中k个顶点至少关联 kt条边,这 kt条边至少关联V2中的k个顶点,于是若G满足t条件,则。
匈牙利算法,由埃德蒙德斯于1965年提出,专为解决二部图最大匹配问题而简化最大流算法它巧妙地利用二部图特点,简化匹配过程,避免了复杂网络图模型的使用二部图匹配问题无需区分源点与汇点,不考虑边的方向性,因此,算法优化,简化流程,成为高效二分匹配解决方案基本流程如下初始化最大匹配为。